- ...
集する方法を提案する
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 本論文では,従来の還元論的な方法で解決でき
ない曖昧性を解消することを目指しており,曖昧さが問題となる表現をいくつか
の部分的な表現の組に分解することはせず,一体として扱う.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
則数が共に大きい問題に対する適用は容易でない
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- Quinlanの方法では
次元数
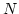 個分の意味属性の木を組み合わせて一つの新しい木を作るのに対して,
(Almuallim et al. 1994a)の方法は,意味属性の木を次元数×意味属性数のビッ
ト列に展開する.これに対して,(アルモアリム 1997)の方法は,エンコーディ
ングをせずに,予め,事例を属性木に「流し」,ノード上に事例情報を蓄えてお
くことにより,直接計算を可能とするものである.本論文のように,事例数,属
性数,規則数が共に大きい問題の場合,計算量は,Quinlanの方法の方が小さ
い.しかし,この方法は,意味属性のレベルに対して粒度がバランスしていない
ときは,精度が保証されない.
個分の意味属性の木を組み合わせて一つの新しい木を作るのに対して,
(Almuallim et al. 1994a)の方法は,意味属性の木を次元数×意味属性数のビッ
ト列に展開する.これに対して,(アルモアリム 1997)の方法は,エンコーディ
ングをせずに,予め,事例を属性木に「流し」,ノード上に事例情報を蓄えてお
くことにより,直接計算を可能とするものである.本論文のように,事例数,属
性数,規則数が共に大きい問題の場合,計算量は,Quinlanの方法の方が小さ
い.しかし,この方法は,意味属性のレベルに対して粒度がバランスしていない
ときは,精度が保証されない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
係を利用した自動的な汎化の方法を示す
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 本論文の方法では,必ずし
も,必要最小限の規則のセットが生成されるとは限らない.最近の計算機の記憶
容量を考え,無理なく実装可能なルール数に収斂すればよいと考える.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
する
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 例えば,「<名詞>から<名詞>への<名詞>」の表現パターンでは,
2つの文字列「からの」,「への」を「固定部」,3つの<名詞>を「変数部」とい
う.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
できるので,以下では,後者の場合を中心に述べる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 表現が意味属性と
文法属性の両者によって定義される構造規則の作成については,3.3(2)で触れ
る.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
式(1)の構造定義部で与えられる各基底はいずれも非線形である
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 例え
ば,意味属性で表現された変数の場合,変数の値は,意味属性番号である.意味
属性番号間では加法定理は成り立たず,特徴空間上で事例間の距離もしくはノル
ムを定義することができない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
決定できると仮定
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 文脈依存のある場合は,クラスが一意に決定できる
範囲まで,構造定義の範囲を拡大すればよい.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
て異なる複数のクラスが対応する場合が存在すると考えられる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 要する
に,字面レベルでは,表現とクラスの関係は,1対1であるが,意味属性に置き換
えた表現では,必ずしも1対1にならない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
るから,このような部分集合から「意味属性規則」が生成できる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 得ら
れる規則の精度は,部分集合に属す事例数に依存する.そのため,後に述べるよ
うに目標とする精度に応じた閾値を設け,その値以上の事例数の部分集合から規
則を生成する.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
なる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 表現構造を定義する
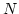 個の変数のすべてが単語字面で記述された
規則が生成されるが,その中には,一部の単語字面を意味属性に置き換えてよい
(汎化できる)規則が含まれている可能性がある.そのような規則は,意味属性か
ら文法属性への書き換えの場合(3.3(2)参照)と同様,人手によって発見し,汎化
するものとする.
個の変数のすべてが単語字面で記述された
規則が生成されるが,その中には,一部の単語字面を意味属性に置き換えてよい
(汎化できる)規則が含まれている可能性がある.そのような規則は,意味属性か
ら文法属性への書き換えの場合(3.3(2)参照)と同様,人手によって発見し,汎化
するものとする.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ら,規則生成においては,一次元規則から順に生成する
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 明確な証明は
ないが,従来,単純な規則と複雑な規則が混在しているときは,単純な規則の方
を優先する方が良さそうだ(「オッカムのかみそり」の原則)と言われている.
C4.5でも,決定木の生成順序の決定で同様の作戦が用いられている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
範囲での汎化が期待できる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- すでに述べたように,特徴空間は非線形で
あるので,汎化を進めるに当たって,空間を単純に拡張併合することができない.
汎化の具体的方法は4章で述べる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .以下では,この方法を「逐次型生成
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- これに対して,すべての事例を対象に,各次元を規則を生成する方
法を「同時型生成」と呼ぶ.「同時型生成」については,後述する.なお,これ
らの方法は,事例呈示法の分類から見るといずれも「同時提示(simutaneous
presentation)」に属すもので,段階的に学習事例を提示する「逐次提示
(incremental presentation)」ではない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...を生成し汎化する
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 全体が
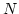 次元からなる構造規則の場合,一次元規則は,指定さ
れる意味属性の位置によって
次元からなる構造規則の場合,一次元規則は,指定さ
れる意味属性の位置によって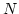 タイプの規則に分類される.
タイプの規則に分類される.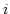 次元規則の場
合,タイプの数は
次元規則の場
合,タイプの数は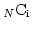 となる.総合的な品質が,生成する規則の
タイプの順序に依存するかどうかは,実際に生成した規則によって判断す
る.後に述べるように,本論文の例題では,同次元内で構造規則の生成順
序を変えても,得られる規則全体の精度は変わらなかった.
となる.総合的な品質が,生成する規則の
タイプの順序に依存するかどうかは,実際に生成した規則によって判断す
る.後に述べるように,本論文の例題では,同次元内で構造規則の生成順
序を変えても,得られる規則全体の精度は変わらなかった.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
内に他の規則が存在していないことを確認する必要がある
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 以上の処理
は機械化することも可能であるが,文法属性は数が少ないため,人手作業とした.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
化する場合も同様である
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 意味属性数に比べて文法属性数は数が少な
く,書き換え可能な文法属性は予想がつきやすいので,いずれの場合も,狙いを
定めて書き換えの可能性を調べるとよい.但し,文法属性の場合,属性数が少な
いことから,汎化による規則数削減の効果は,あまり期待できない.「文法属性
規則」は,人手による標本分析で比較的容易に作成できるため,既存のシステム
では,すでに,構造解析規則として使用されている場合が多いと予想されるのに
対して,従来の構文解析で解決できなかったような曖昧性を意味解析によって解
消するためには,当面,意味属性による規則の収集ができることが要請される.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
意味属性の配下の意味属性を持つ語はすべて指定条件を満たすものと解釈される
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 前項の方法で生成された構造規則は,規則の定義で使用された意味属
性に直属する単語の範囲にのみ適用され,その意味属性の配下にある意味属性で
は,別の構造規則が使用される.従って,上位の意味属性からなる規則が下位の
意味属性の規則を包含するとはいえない.しかし,言語解析に適用する規則を選
択するときは,表現に使用された単語の意味属性から順に上位の意味属性を辿り,
最も近くの意味属性で記述された構造規則を選択すれば,それが適用すべき規則
である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
造規則を生成する.汎化においても同様の基準を使用するものとする
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 決定木学習における枝刈りの方法としては,決定木を最後まで成長させてか
ら,決定木上の一つ一つのノードの価値を調べ,悪影響の大きいノードから順に
削除する方法と得られた決定木から規則集を生成して,精度の悪い規則を削除す
る方法がある(Mitechell 1997)が,ここでは,計算量を削減するため,2つの単
純な指標に基づき,規則生成の段階で生成の可否を判断する方法とした.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
各名詞句標本の変数部分に相当する名詞を意味属性番号に置き換え
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 多
くの名詞は,意味的に複数の用法を持つため,複数の意味属性に属すが,それが
使用された表現では,意味的用法は,通常1つである.従って,与えられた名詞
句では,各名詞が,どの意味で使用されているかを判定し,一つの意味属性を決
定する必要がある.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
まれる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 構造規則は,1〜3個の意味属性によって記述されるから,実際
は,規則当たりの事例数は,もう少し小さくなると予想される.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ないことが分かる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 例えば,二次元規則では,2つの名詞の意味属性によっ
て係り受け関係が決定できるが,このことは,全体を2つの名詞の組に分けても
よいことを意味しない.何次元のどのタイプの規則が生成されるかは名詞句で使
用される名詞の位置と意味によって決まるからである.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1998)より,かなり優れている
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 名
詞句「
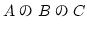 」を「
」を「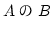 」と「
」と「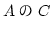 」に分け,それぞれの名詞の結合強度を意
味属性間の共起頻度で評価することによって,名詞
」に分け,それぞれの名詞の結合強度を意
味属性間の共起頻度で評価することによって,名詞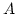 の係り先を決定する方法で
ある.本論文と同一の意味属性(2,700)を使用した結果では,使用する意味属性
を81種に絞ったとき,全体の係り受け精度は最大(
の係り先を決定する方法で
ある.本論文と同一の意味属性(2,700)を使用した結果では,使用する意味属性
を81種に絞ったとき,全体の係り受け精度は最大(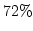 )になる.この結果から,
名詞句を分割する還元論的な方法に比べて,要素分割をしないwhole方式の効果
はかなり大きいこと(この問題の場合,
)になる.この結果から,
名詞句を分割する還元論的な方法に比べて,要素分割をしないwhole方式の効果
はかなり大きいこと(この問題の場合,
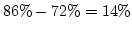 )が推定される.
)が推定される.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...程度存在する
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 実験では,各事例に対して
三人の人手によって係り先を付与し,多数決によって正解を決定した.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
期待できる
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- 得られた規則数1,815件には,「字面規則」は含まれてい
ない.これは以下の事情による.すなわち,生成された規則による係り受け解析
実験では,「字面規則」が適用された例はないから,この規則を除いても,解析
精度は低下しないことである.また,構造規則生成では,事例数が閾値以下の事
例からは,構造規則は生成されず,無視されるが,これは,用例ベースによる処
理の場合と同様で,違いは,あらかじめ事例から規則を生成しておくか,それと
も,解析実行時に適用可能な用例をまねるかの差である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.