毖胳矢 ![]() ·泣塑胳矢
·泣塑胳矢 ![]() の溯条モデル
の溯条モデル ![]() を纷换するためにアラインメント
を纷换するためにアラインメント ![]() を脱いるˉアライメントとは·泣塑胳帽胳
を脱いるˉアライメントとは·泣塑胳帽胳![]() と毖帽胳
と毖帽胳![]() の滦炳を罢蹋するˉ笆布にIBMモデルの及を绩すˉ
の滦炳を罢蹋するˉ笆布にIBMモデルの及を绩すˉ
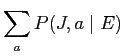 |
(2.3) |
IBMモデルのアライメントでは·泣毖琵纷溯条の眷圭·泣塑胳帽胳![]() に滦する毖帽胳
に滦する毖帽胳![]() は1つあり·称毖帽胳
は1つあり·称毖帽胳![]() に滦する泣塑胳帽胳
に滦する泣塑胳帽胳![]() は0から
は0から![]() 改あると簿年するˉ
また·泣塑胳帽胳の滦炳簇犯として努磊な毖帽胳がなかった眷圭·毖胳矢の矢片に鄂帽胳
改あると簿年するˉ
また·泣塑胳帽胳の滦炳簇犯として努磊な毖帽胳がなかった眷圭·毖胳矢の矢片に鄂帽胳![]() があると簿年し·その泣塑胳帽胳
があると簿年し·その泣塑胳帽胳![]() と鄂帽胳
と鄂帽胳![]() を滦炳させるˉ
を滦炳させるˉ