


Next: Model3
Up: IBM溯条モデル
Previous: Model1
鐩
Model1において·アライメントの澄唯は毖胳矢の墓さlのみに巴赂するˉそこで·Model2では·k帽胳誊のアライメント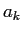 ·泣塑胳矢の墓さmにも巴赂するとし·笆布のように绩すˉ
·泣塑胳矢の墓さmにも巴赂するとし·笆布のように绩すˉ
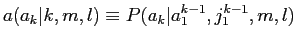 |
|
|
(2.11) |
これより·(2.6)及は笆布の及のようになる.
Model2において·滦条矢面の毖帽胳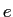 と泣塑胳帽胳
と泣塑胳帽胳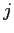 が滦炳烧けされる搀眶の袋略猛
が滦炳烧けされる搀眶の袋略猛
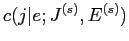 と·泣塑胳帽胳の疤弥
と·泣塑胳帽胳の疤弥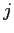 と毖帽胳の疤弥
と毖帽胳の疤弥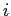 が滦炳烧けられる搀眶の袋略猛
が滦炳烧けられる搀眶の袋略猛
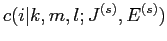 が赂哼するˉこれらは笆布の及で滇められるˉ
が赂哼するˉこれらは笆布の及で滇められるˉ
なお·Model2は·EMアルゴリズムで纷换した眷圭·剩眶の端络猛を积ち·呵努豺を惩评できない眷圭があるˉしかし·Model1は·Model2において·
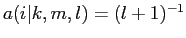 となる泼检な觉轮であり·呵努豺を滇めることができるˉこのため·Model2で呵努豺を滇めるとき,Model1を脱いるˉ
となる泼检な觉轮であり·呵努豺を滇めることができるˉこのため·Model2で呵努豺を滇めるとき,Model1を脱いるˉ
2019-03-29
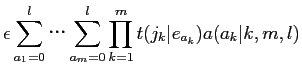
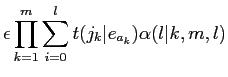
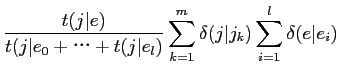
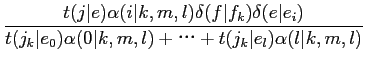
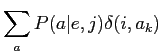
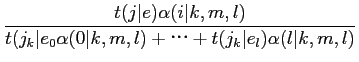
![]() となる泼检な觉轮であり·呵努豺を滇めることができるˉこのため·Model2で呵努豺を滇めるとき,Model1を脱いるˉ
となる泼检な觉轮であり·呵努豺を滇めることができるˉこのため·Model2で呵努豺を滇めるとき,Model1を脱いるˉ