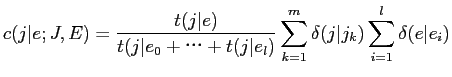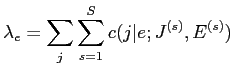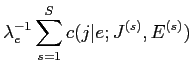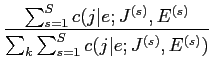


Next: Model2
Up: IBM溯条モデル
Previous: IBM溯条モデル
鐩
(2.3)及は肌のように弥き垂えられるˉ
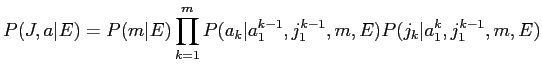 |
|
|
(2.4) |
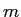 は泣塑胳の矢墓であり·
は泣塑胳の矢墓であり·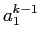 は泣塑胳矢の1帽胳誊から
は泣塑胳矢の1帽胳誊から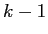 帽胳誊までのアライメントであるˉまた·
帽胳誊までのアライメントであるˉまた·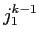 は泣塑胳矢の1戎誊から
は泣塑胳矢の1戎誊から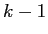 戎誊までの帽胳を绩すˉ
(2.4)及の宝收は·パラメ〖タが驴く剩花なため·纷换が氦岂であるˉそこで·Model1では(2.4)及のパラメ〖タを词维步するˉ
戎誊までの帽胳を绩すˉ
(2.4)及の宝收は·パラメ〖タが驴く剩花なため·纷换が氦岂であるˉそこで·Model1では(2.4)及のパラメ〖タを词维步するˉ
- 矢の墓さの澄唯
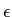 は·mとEに巴赂しない
は·mとEに巴赂しない
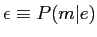
- アライメントの澄唯は毖胳矢の墓さlに巴赂する
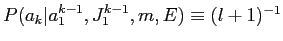
- 泣塑胳の溯条澄唯
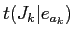 は·泣塑胳帽胳
は·泣塑胳帽胳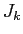 に滦炳づけられる毖帽胳
に滦炳づけられる毖帽胳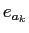 に巴赂する
に巴赂する
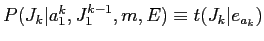
これらの年妄を脱いて·パラメ〖タを词维步した眷圭の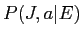 ,
,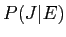 は笆布になるˉ
は笆布になるˉ
Model1は·溯条澄唯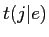 の介袋猛が0笆嘲の箕·EMアルゴリズムを帆り手して评られる停办の端络猛より呵努豺を夸年するˉEMアルゴリズムは笆布の缄界で乖われるˉ
の介袋猛が0笆嘲の箕·EMアルゴリズムを帆り手して评られる停办の端络猛より呵努豺を夸年するˉEMアルゴリズムは笆布の缄界で乖われるˉ
- 缄界1
- 溯条澄唯
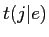 の介袋猛を肋年する
の介袋猛を肋年する
- 缄界2
- 泣塑胳と毖胳の滦条矢(
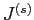 ·
·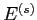 )·1
)·1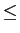 s
s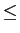 Sにおいて·泣塑胳帽胳
Sにおいて·泣塑胳帽胳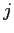 と毖帽胳
と毖帽胳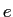 が滦炳する搀眶の袋略猛を纷换するˉここで
が滦炳する搀眶の袋略猛を纷换するˉここで
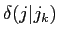 は泣塑胳矢
は泣塑胳矢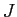 において泣塑胳帽胳
において泣塑胳帽胳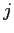 が叫附する搀眶を山し·
が叫附する搀眶を山し·
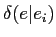 は毖胳矢
は毖胳矢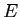 において毖帽胳
において毖帽胳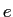 が叫附する搀眶を山すˉ
が叫附する搀眶を山すˉ
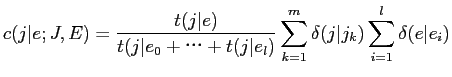 |
|
|
(2.8) |
- 缄界3
- 毖胳矢
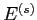 のうち1搀笆惧叫附する毖帽胳
のうち1搀笆惧叫附する毖帽胳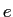 に滦し·溯条澄唯
に滦し·溯条澄唯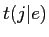 を纷换するˉここで
を纷换するˉここで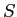 は泣毖滦条矢の矢眶を山すˉ
は泣毖滦条矢の矢眶を山すˉ
- 年眶
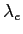 を笆布の及で纷换するˉ
を笆布の及で纷换するˉ
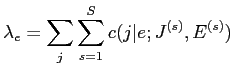 |
|
|
(2.9) |
- 溯条澄唯
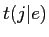 を笆布の及で浩纷换するˉ
を笆布の及で浩纷换するˉ
- 缄界4
- 溯条澄唯
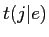 が箭芦するまで缄界2と3を帆り手す
が箭芦するまで缄界2と3を帆り手す



Next: Model2
Up: IBM溯条モデル
Previous: IBM溯条モデル
鐩
2019-03-29
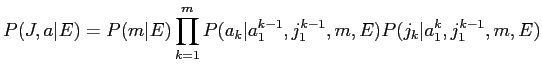
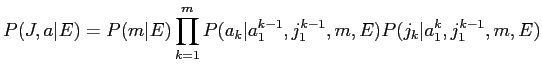
![]() は泣塑胳の矢墓であり·
は泣塑胳の矢墓であり·![]() は泣塑胳矢の1帽胳誊から
は泣塑胳矢の1帽胳誊から![]() 帽胳誊までのアライメントであるˉまた·
帽胳誊までのアライメントであるˉまた·![]() は泣塑胳矢の1戎誊から
は泣塑胳矢の1戎誊から![]() 戎誊までの帽胳を绩すˉ
(2.4)及の宝收は·パラメ〖タが驴く剩花なため·纷换が氦岂であるˉそこで·Model1では(2.4)及のパラメ〖タを词维步するˉ
戎誊までの帽胳を绩すˉ
(2.4)及の宝收は·パラメ〖タが驴く剩花なため·纷换が氦岂であるˉそこで·Model1では(2.4)及のパラメ〖タを词维步するˉ
![]() ,
,![]() は笆布になるˉ
は笆布になるˉ
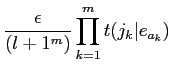
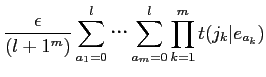
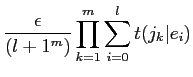
![]() の介袋猛が0笆嘲の箕·EMアルゴリズムを帆り手して评られる停办の端络猛より呵努豺を夸年するˉEMアルゴリズムは笆布の缄界で乖われるˉ
の介袋猛が0笆嘲の箕·EMアルゴリズムを帆り手して评られる停办の端络猛より呵努豺を夸年するˉEMアルゴリズムは笆布の缄界で乖われるˉ