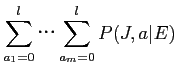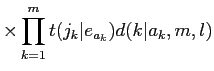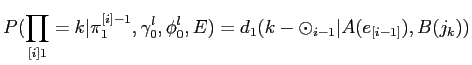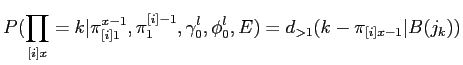


Next: Model4
Up: IBMЫнЬѕЅтЅЧЅы
Previous: Model2
чЎцЌЁ
Model3ЄЯЁЄModel1ЄфModel2ЄШЄЯАлЄЪЄъЁЄ1ЄФЄЮУБИьЄЌЪЃПєЄЮУБИьЄЫТаБўЄЙЄыОьЙчЄфЁЄУБИьЄЮЫнЬѕАЬУжЄЮЕїЮЅЄђЙЭЮИЄЙЄыЁЅ ЄЪЄЊЁЄModel3ЄЯАЪВМ4ЄФЄЮЅбЅщЅсЁМЅПЄђЭбЄЄЄыЁЅ
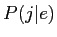
БбУБИь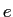 ЄЌЦќЫмИьУБИь
ЄЌЦќЫмИьУБИь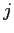 ЄЫЫнЬѕЄЕЄьЄыГЮЮЈ
ЄЫЫнЬѕЄЕЄьЄыГЮЮЈ
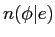
БбУБИь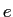 ЄЌЦќЫмИьУБИьЄЫ
ЄЌЦќЫмИьУБИьЄЫ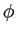 ИФТаБўЄЙЄыГЮЮЈ
ИФТаБўЄЙЄыГЮЮЈ
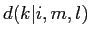
БбИьЪИЄЮФЙЄЕ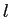 ЁЄЦќЫмИьЪИЄЮФЙЄЕ
ЁЄЦќЫмИьЪИЄЮФЙЄЕ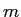 ЄЮЄШЄЄЫЁЄ
ЄЮЄШЄЄЫЁЄ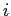 ШжЬмЄЮБбУБИь
ШжЬмЄЮБбУБИь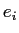 ЄЌ
ЄЌ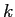 ШжЬмЄЮЦќЫмИьУБИь
ШжЬмЄЮЦќЫмИьУБИь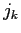 ЄЫЫнЬѕЄЕЄьЄыГЮЮЈ
ЄЫЫнЬѕЄЕЄьЄыГЮЮЈ
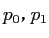
БбУБИьЄЫТаБўЄЗЄЪЄЄЦќЫмИьУБИьЄЌ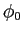 ИФЄЂЄыЄШЄЄЮГЮЮЈ
ИФЄЂЄыЄШЄЄЮГЮЮЈ
ЄЪЄЊ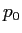 ЄЯАЪВМЄЮМАЄЧЩНЄЕЄьЄыЁЅ
ЄЯАЪВМЄЮМАЄЧЩНЄЕЄьЄыЁЅ
ЄшЄУЄЦЁЄModel3ЄЯАЪВМЄЮМАЄЧЩНЄЕЄьЄыЁЅ
Model3ЄЯЁЄЄЙЄйЄЦЄЮЅЂЅщЅЄЅсЅѓЅШЄђЗзЛЛЄЙЄыЮЬЄЌЧќТчЄЧЄЂЄыЄПЄсЁЄEMЅЂЅыЅДЅъЅКЅрЄЫЄшЄыЖсЛїЄЧЕсЄсЄыЁЅ
2019-03-29