Next: ・モデル3 Up: IBM翻訳モデル Previous: ・モデル1 目次
| (2.9) |
この関係からモデル1における(2.4)式は, 以下の式に変換できる.
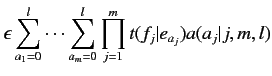 |
(2.10) | ||
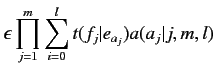 |
(2.11) |
モデル2では, 期待値は
![]() と
と
![]() の2つが存在する.以下の式から求められる.
の2つが存在する.以下の式から求められる.
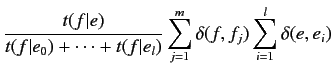 |
(2.12) | ||
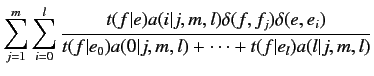 |
(2.13) | ||
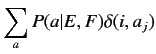 |
(2.14) | ||
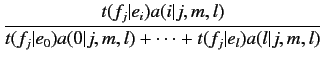 |
(2.15) |
モデル2では, EMアルゴリズムで計算すると複数の極大値が算出され, 最適解が
得られない可能性がある.モデル1では
![]() となるモデル
2の特殊な場合であると考えられる.したがって, モデル1を用いることで最適解
を得ることができる.
となるモデル
2の特殊な場合であると考えられる.したがって, モデル1を用いることで最適解
を得ることができる.