Next: ・モデル2 Up: IBM翻訳モデル Previous: IBM翻訳モデル 目次
パラメータの簡略化を行うことで, ![]() と
と![]() は以下の式で表
される.
は以下の式で表
される.
モデル1では翻訳確率![]() の初期値が0以外の場合,
Expectation-Maximization(EM)アルゴリズムを繰り返し行うことで得られる期待
値を用いて最適解を推定する.EMアルゴリズムの手順を以下に示す.
の初期値が0以外の場合,
Expectation-Maximization(EM)アルゴリズムを繰り返し行うことで得られる期待
値を用いて最適解を推定する.EMアルゴリズムの手順を以下に示す.
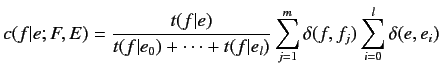 |
(2.6) |
![]() はフランス語文
はフランス語文![]() 中で仏単語
中で仏単語
![]() が出現する回数,
が出現する回数,
![]() は英語文
は英語文![]() 中で英単語
中で英単語![]() が出現する回数を表している.
が出現する回数を表している.
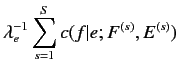 |
|||
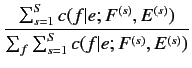 |
(2.8) |