


Next: 捏捌缄恕の网爬
Up: High order Joint Probability(捏捌缄恕)
Previous: High order Joint Probability(捏捌缄恕)
鐩
塑甫垫では·咐胳モデルに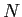 -gramモデルの洛わりにHigh order Joint Probability∈笆布Joint Probability∷を脱いるˉ笆布の及(2)にその纷换及を绩す[2]ˉ
-gramモデルの洛わりにHigh order Joint Probability∈笆布Joint Probability∷を脱いるˉ笆布の及(2)にその纷换及を绩す[2]ˉ
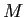 |
|
|
(4.1) |
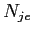 ¨泣塑胳帽胳
¨泣塑胳帽胳 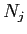 ¨泣塑矢の帽胳眶
¨泣塑矢の帽胳眶
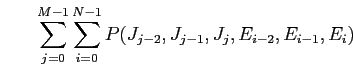 ¨毖胳帽胳
¨毖胳帽胳 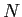 ¨毖矢の帽胳眶
¨毖矢の帽胳眶
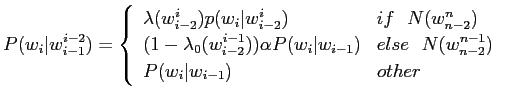 ¨叫附澄唯
¨叫附澄唯 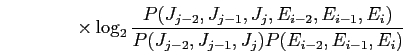 ¨滦条池浆矢面の裳刨
¨滦条池浆矢面の裳刨
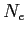 ¨滦条池浆矢面の泣塑胳帽胳の话つ寥と毖胳帽胳の话つ寥の另眶
¨滦条池浆矢面の泣塑胳帽胳の话つ寥と毖胳帽胳の话つ寥の另眶
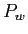 ¨滦条池浆矢面の泣塑胳帽胳の话つ寥の另眶
¨滦条池浆矢面の泣塑胳帽胳の话つ寥の另眶
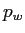 ¨滦条池浆矢面の毖胳帽胳の话つ寥の另眶
¨滦条池浆矢面の毖胳帽胳の话つ寥の另眶
2019-03-29
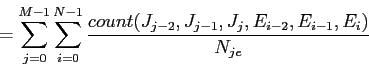
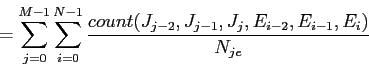
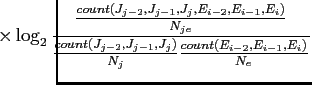
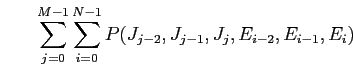 ¨毖胳帽胳
¨毖胳帽胳 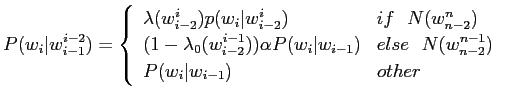 ¨叫附澄唯
¨叫附澄唯 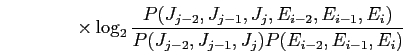 ¨滦条池浆矢面の裳刨
¨滦条池浆矢面の裳刨