 |
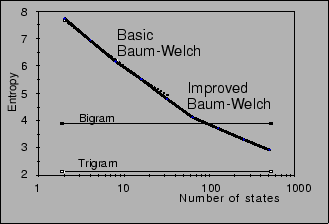
To understand how the Ergodic HMM proved adequate, we studied the entropy of the Ergodic HMM. Figure 2 shows these results. In this figure, the vertical axis represents entropy and the horizontal axis represents the number of states. The line of dots is the result for the basic Baum-Welch algorithm and the thick line is that for the improved Baum-Welch algorithm. For comparison purposes, the calculated entropy of word bigram and trigram models are included.
In this figure, the difference between the basic Baum-Welch algorithm and the improved Baum-Welch algorithm is small. This means that the proposed algorithm can perform training like the basic Baum-Welch algorithm with lower the memory requirements and computational costs. And as the number of states increases, the entropy decreases. The entropy of the 128-state Ergodic HMM is lower than that of the word bigram models. However, the perplexity of the 512-state Ergodic HMM is higher than that of the word trigram models. It is possible though that if the number of states were increased, the entropy of the Ergodic HMM would have lowered that of the word trigram models.