手順3 : 文のクラスタリング
2.1節の手順3では,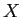 -means法[4][5]というクラスタリング手法を用いて文をクラスタリングする.
-means法[4][5]というクラスタリング手法を用いて文をクラスタリングする.
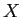 -means法は,図2.2のようにK=2での
-means法は,図2.2のようにK=2での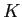 -means法による分割を繰り返し,ベイズ情報量
-means法による分割を繰り返し,ベイズ情報量 によって分割を停止するかを判定することで,クラスタ数を自動で決定するクラスタリング手法である.分割前のベイズ情報量
によって分割を停止するかを判定することで,クラスタ数を自動で決定するクラスタリング手法である.分割前のベイズ情報量 ,分割後のベイズ情報量
,分割後のベイズ情報量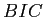 に対し,
に対し,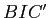 ならば分割を停止する.
ならば分割を停止する.
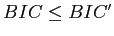 変量正規分布を
変量正規分布を
と仮定すると, は以下のように定義される.ここで
は以下のように定義される.ここで
![$\hat{\theta_i}=[\hat{\mu_i},\hat{V_i}]$](img13.png) は,
は,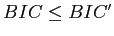 変量正規分布の最尤推定値とし,
変量正規分布の最尤推定値とし,
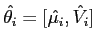 は
は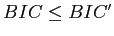 次の平均値ベクトル,
次の平均値ベクトル,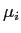 は
は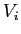 の分散共分散行列である.
の分散共分散行列である.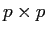 はパラメータ空間の次元数で,
はパラメータ空間の次元数で,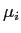 の共分散を無視すれば
の共分散を無視すれば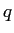 であり,無視しなければ
であり,無視しなければ である.
である.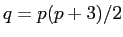 は尤度関数で
は尤度関数で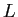 である.
である.
また,分割後の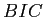 は以下のように定義される.ここで
は以下のように定義される.ここで
![$\hat{\theta_i'}=[\hat{\theta_i^1},\hat{\theta_i^2}]$](img23.png) は,分割後の2つの各クラスタにおける
は,分割後の2つの各クラスタにおける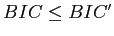 変量正規分布の最尤推定値とする.共分散を無視すると,各
変量正規分布の最尤推定値とする.共分散を無視すると,各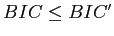 に対し平均と分散の2つのパラメータが存在するので,
に対し平均と分散の2つのパラメータが存在するので,
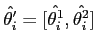 であり,無視しなければ
であり,無視しなければ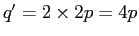 である.
である.
図:
 -means法のイメージ
-means法のイメージ
|
|
 によって分割を停止するかを判定することで,クラスタ数を自動で決定するクラスタリング手法である.分割前のベイズ情報量
によって分割を停止するかを判定することで,クラスタ数を自動で決定するクラスタリング手法である.分割前のベイズ情報量 ,分割後のベイズ情報量
,分割後のベイズ情報量 は以下のように定義される.ここで
は以下のように定義される.ここで
![$\hat{\theta_i}=[\hat{\mu_i},\hat{V_i}]$](img13.png) は,
は,