Next: 手順5 : 列の項目名の付与 Up: 従来手法 Previous: 手順3 : 文のクラスタリング 目次
クラスタリング結果を整理した表の列には,表2.1の列1のように関連する文だけで構成される重要度の高い列もあれば,列2のように関連しない文が混在した重要度の低い列もある.
まず密集率について, 番目の列の密集率
番目の列の密集率![]() を式2.1のように定める.
ここで,
を式2.1のように定める.
ここで,![]() は
は 番目の列に含まれる文の総数であり,
番目の列に含まれる文の総数であり,![]() は
は 番目の列に含まれる
番目の列に含まれる![]() 番目の文のベクトルであり,
番目の文のベクトルであり, ![]() は
は 番目の列に含まれる文のベクトルの平均である.
番目の列に含まれる文のベクトルの平均である.
式2.1で求めた列の密集率![]() を,式2.2を用いて,最小値が0,最大値が1になるように正規化する.
ここで,
を,式2.2を用いて,最小値が0,最大値が1になるように正規化する.
ここで,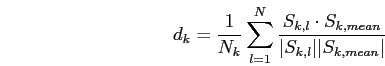 は
は 番目の列の正規化された列の密集率であり,
番目の列の正規化された列の密集率であり,![]() は列の総数である.
は列の総数である.
| (2.3) |
| (2.4) |
次に文書カバー率について, 番目の列の文書カバー率
番目の列の文書カバー率![]() を式2.5のように定める.
を式2.5のように定める.
![]() は
は 番目の列において文を抽出できた文書の数であり,
番目の列において文を抽出できた文書の数であり,![]() は文書の総数である.
は文書の総数である.
式2.5で求めた文書カバー率![]() を,式2.6を用いて,最小値が0,最大値が1になるように正規化する.
ここで,
を,式2.6を用いて,最小値が0,最大値が1になるように正規化する.
ここで,![]() は
は 番目の列の正規化された文書カバー率であり,
番目の列の正規化された文書カバー率であり,![]() は列の総数である
は列の総数である
| (2.7) |
| (2.8) |
 番目の列の重要度
番目の列の重要度![]() を式2.9のように定義する.
を式2.9のように定義する.