Upper Tail 法はMojena[8]によって提案された,階層クラスタリングの結果に対し統計的な停止規則に基づいて最適なクラスタ数を決定する手法である.
Upper Tail 法では,まず,クラスタ数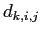 が2〜
が2〜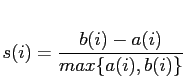 となる場合の,それぞれのクラスタリング結果に対し,基準値
となる場合の,それぞれのクラスタリング結果に対し,基準値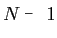 を求める.
ここで,
を求める.
ここで,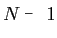 はクラスタ数
はクラスタ数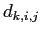 でのクラスタリング結果における各クラスタの重心点間の距離のうち,最小の距離を表す.
次に
でのクラスタリング結果における各クラスタの重心点間の距離のうち,最小の距離を表す.
次に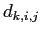 の値を2からはじめて,以下の条件
の値を2からはじめて,以下の条件
を満たさなくなるまで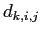 の値を1ずつ増やしていく.停止したときの
の値を1ずつ増やしていく.停止したときの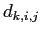 が最適なクラスタ数として選ばれる.
ここで,
が最適なクラスタ数として選ばれる.
ここで, と
と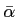 はそれぞれ,全ての基準値
はそれぞれ,全ての基準値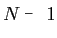 の平均と不偏分散の平方根を表す.
の平均と不偏分散の平方根を表す.
 の値については,Mojena[8]では,データ数が60〜120の場合,2〜4の値を用いている.
また,志津ら[9]は1群のデータ数が30〜50前後の場合は
の値については,Mojena[8]では,データ数が60〜120の場合,2〜4の値を用いている.
また,志津ら[9]は1群のデータ数が30〜50前後の場合は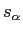 がよいと報告している.
これらを参考に,今回は1群のデータ数が文書数以下(20以下)になると仮定して,
がよいと報告している.
これらを参考に,今回は1群のデータ数が文書数以下(20以下)になると仮定して,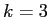 で実験を行う.
で実験を行う.
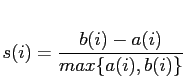 となる場合の,それぞれのクラスタリング結果に対し,基準値
となる場合の,それぞれのクラスタリング結果に対し,基準値 の値については,Mojena[8]では,データ数が60〜120の場合,2〜4の値を用いている.
また,志津ら[9]は1群のデータ数が30〜50前後の場合は
の値については,Mojena[8]では,データ数が60〜120の場合,2〜4の値を用いている.
また,志津ら[9]は1群のデータ数が30〜50前後の場合は