シルエット分析[7]は,クラスタ内のデータの凝集性とクラスタ間の離散性に基づく指標である.
シルエット分析では,クラスタ数ごとに,全てのデータのシルエット係数を計算し,この平均値が最大となるときのクラスタ数を選択する.
データ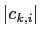 のシルエット係数
のシルエット係数 は式5.1で表される.
ここで,
は式5.1で表される.
ここで,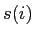 はデータ
はデータ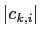 とデータ
とデータ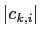 の属するクラスタに含まれる各データとの距離の平均,
の属するクラスタに含まれる各データとの距離の平均,
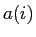 はデータ
はデータ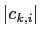 の属さないクラスタのうち,データ
の属さないクラスタのうち,データ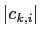 と最も距離の近いクラスタに含まれる各データとデータ
と最も距離の近いクラスタに含まれる各データとデータ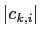 との距離の平均を表す.
ここで,データ
との距離の平均を表す.
ここで,データ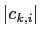 と最も距離の近いクラスタは,データ
と最も距離の近いクラスタは,データ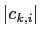 とクラスタに含まれる各データとの距離の平均が最小となる場合のクラスタである.
また,
とクラスタに含まれる各データとの距離の平均が最小となる場合のクラスタである.
また,
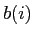 は
は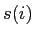 と
と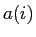 のうち,大きい方の値を表す.
のうち,大きい方の値を表す.
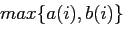 |
(5.1) |
 は式5.1で表される.
ここで,
は式5.1で表される.
ここで,