


Next: GIZA++
Up: 従来手法
Previous: Model5
目次
単語アライメントの問題について,Stephanら[4]による1次の隠れマルコフモデル(以下、HMM)がある.以下,Stephanらの論文を参照して記述している.HMMの重要な要素は,アライメントの確率を単語アライメントの絶対位置ではなく,相対位置に依存させることである.つまり,インデックス自体ではなく,単語の位置のインデックスの違いを考慮する.
HMMは仏英翻訳を前提としているが,本研究では日英翻訳を扱っているため,日英翻訳を前提に説明する.日本語の文字列
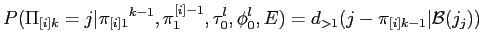 が与えられる.これは英語の文字列
が与えられる.これは英語の文字列
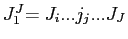 に変換される. 考えられる全ての英語の文字列の中から,ベイズの決定規則によって与えられる最も高い確率を持つものを選択する.
に変換される. 考えられる全ての英語の文字列の中から,ベイズの決定規則によって与えられる最も高い確率を持つものを選択する.
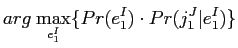 は目的言語の言語モデルであるが,
は目的言語の言語モデルであるが,
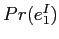 は,文字列翻訳モデルである.
は,文字列翻訳モデルである.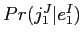
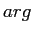 操作は,検索問題を示す.文字列翻訳確率
操作は,検索問題を示す.文字列翻訳確率
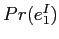 をモデル化するために,確率依存性に構造を導入する.
をモデル化するために,確率依存性に構造を導入する.
ここでは,混合ベースのアライメントモデルについて説明する.このモデルは,後で提示するHMMの基本アライメントの参照として使用する.このモデルは,各単語jの確率について,jの結合確率を積に分解したものに基づいている.
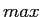 |
|
|
(2.22) |
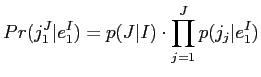 は,正規化のための文の長さの確率である.次のステップは,日本語の単語
は,正規化のための文の長さの確率である.次のステップは,日本語の単語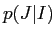 と各英語の単語
と各英語の単語
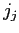 との間の一種のペアワイズ相互作用である.これらの依存関係は,混合分布から取り込まれる.
との間の一種のペアワイズ相互作用である.これらの依存関係は,混合分布から取り込まれる.
全てをまとめると,以下のような混合ベースモデルがある.
![$\displaystyle Pr(j^{J}_{1}\vert e^{I}_{1}) = p(J\vert I)\cdot \prod^{J}_{j=1}\sum^{I}_{i=1}[p(i\vert j,I)\cdot p(j_{j}\vert e_{i})]$](img87.png) |
|
|
(2.25) |
- 文の長さの確率:
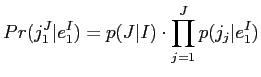
- 混合アライメント確率:
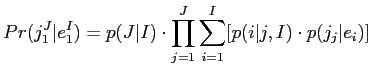
- 翻訳確率:
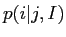
一様アライメント確率を以下に仮定する.
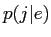 |
|
|
(2.26) |
このモデルはBrownらが提案したIBM Model1と呼ばれる[3].翻訳確率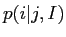 を学習するために,
を学習するために,
![$ [j^{j_{s}}_{1};e^{I_{s}}_{1}],s = 1, ..., S$](img91.png) からなる対訳コーパスを使用する.最大尤度基準を使用して,以下の反復方程式を得る.
からなる対訳コーパスを使用する.最大尤度基準を使用して,以下の反復方程式を得る.
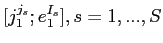 |
|
|
(2.27) |
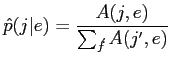 |
|
|
(2.28) |
一様アライメント確率の場合,最適値は1つしかないため,EMアルゴリズムが常に大域的最適値を見つけることができる.一様でないアライメント確率を有する混合アライメントモデル(以下,IBM Model2)は,アライメントパラメータ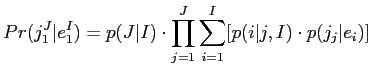 が使用される.したがって,アライメント確率の特定のモデルが使用される.
が使用される.したがって,アライメント確率の特定のモデルが使用される.
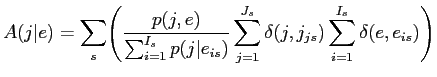 |
|
|
(2.29) |
このモデルを学習するために,最大近似法において最尤基準を使用する.すなわち,尤基準は全アライメントの集合ではなく,最も可能性の高いアライメントのみをカバーする.
![$\displaystyle Pr(j^{J}_{1}\vert e^{I}_{1}) \cong \prod^{J}_{j=1} \underset{i}{\mathrm{max}} [p(i\vert j,I)\cdot p(j_{j}\vert e_{i})]$](img95.png) |
|
|
(2.30) |
学習では,この基準は一連の反復に相当し,各反復は2つのステップで構成されている.
- 位置アライメント:モデルパラメータを大きくして,最も可能性の高い位置アライメントを決定する.
- パラメータ推定:全ての文対に対するアライメント経路に沿って進むと仮定して,モデルパラメータの最大尤度推定を実行する.モデル分布については,これらの相対度数になる.
混合モデルの性質上,隣接する単語位置間の相互作用はない.したがって,各位置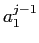 に対する最適位置
に対する最適位置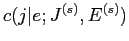 は,隣接位置とは無関係に決定できる.
は,隣接位置とは無関係に決定できる.
次にHMMモデルについて説明する.ここでは,HMM単語単位の代入を記述するために,位置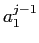 の単語
の単語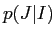 を位置
を位置
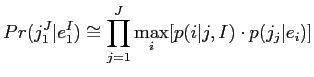 の
の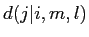 に割り当てる写像
に割り当てる写像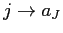 を導入する.位置
を導入する.位置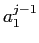 に対するアライメント
に対するアライメント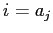 の確率は,前のアラインメント
の確率は,前のアラインメント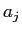 に依存する.
に依存する.
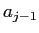 |
|
|
(2.31) |
正規化のために,英語の文の全長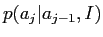 に対する条件付けを含めた.したがって,問題の定式化は,いわゆる隠れマルコフモデルが使用されてきた音声認識における時間整合問題と類似している[5].同じ基本原則を使用して,文対
に対する条件付けを含めた.したがって,問題の定式化は,いわゆる隠れマルコフモデルが使用されてきた音声認識における時間整合問題と類似している[5].同じ基本原則を使用して,文対
![$ [j^{J}_{1};e^{I}_{1}]$](img102.png) に対して,「隠れた」アラインメント
に対して,「隠れた」アラインメント
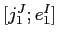 を導入することで書き換えることができる.
を導入することで書き換えることができる.
これまでのところアプローチの基本的な制限はない.ここで,線形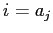 のみへの一次依存性を仮定する.
のみへの一次依存性を仮定する.
ここでさらに,翻訳確率は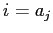 のみに依存し,
のみに依存し,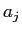 には依存しないと仮定した.まとめると,以下のようなHMMベースモデルがある.
には依存しないと仮定した.まとめると,以下のようなHMMベースモデルがある.
![$\displaystyle Pr(j^{J}_{1}\vert e^{I}_{1}) = \sum{a^{J}_{1}}\prod^{J}_{j=1}[p(a_{j}\vert a_{j-1},I)\cdot p(j_{j}\vert e_{a_j})]$](img109.png) |
|
|
(2.37) |
さらに,HMMアライメント確率:
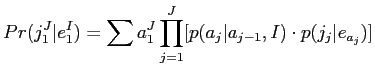 はジャンプ幅
はジャンプ幅
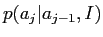 にのみ依存すると仮定する.負でないパラメータの集合
にのみ依存すると仮定する.負でないパラメータの集合
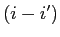 を使って,HMMアライメント確率を以下の形式で書くことができる.
を使って,HMMアライメント確率を以下の形式で書くことができる.
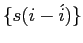 |
|
|
(2.38) |
この形式は,各単語位置
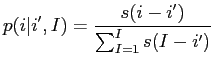 に対して,HMMアライメント確率が正規化制約を満たすことを保証する.混合モデルは一次HMMとは対照的に,ゼロ次モデルとして解釈できる.IBM Model2と同様に,ここでも最大近似を使用する.
に対して,HMMアライメント確率が正規化制約を満たすことを保証する.混合モデルは一次HMMとは対照的に,ゼロ次モデルとして解釈できる.IBM Model2と同様に,ここでも最大近似を使用する.
![$\displaystyle Pr(j^{J}_{1}\vert e^{I}_{1}) \cong \underset{a^{J}_{1}}{\mathrm{max}}\prod^{J}_{j=1}[p(a_{j}\vert a_{j-1},I)\cdot p(j_{j}\vert e_{a_j})]$](img116.png) |
|
|
(2.39) |
この場合,最適アライメントを見出す作業は,混合モデル(IBM Model2)の場合よりも複雑である.したがって,以下の典型的な再帰式がある動的計画法に頼る必要がある.
![$\displaystyle Q(i,j) = p(j_j\vert e_{i}) \underset{i=1,...,I}{\mathrm{max}}[p(i\vert i^{\prime},I)\cdot Q(i^{\prime},J - 1)]$](img117.png) |
|
|
(2.40) |
ここで,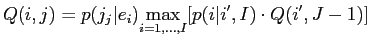 は,音声認識のタイムアライメントのような一種の部分確率である.
は,音声認識のタイムアライメントのような一種の部分確率である.



Next: GIZA++
Up: 従来手法
Previous: Model5
目次
2019-03-08
![]() が与えられる.これは英語の文字列
が与えられる.これは英語の文字列
![]() に変換される. 考えられる全ての英語の文字列の中から,ベイズの決定規則によって与えられる最も高い確率を持つものを選択する.
に変換される. 考えられる全ての英語の文字列の中から,ベイズの決定規則によって与えられる最も高い確率を持つものを選択する.
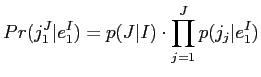 は,正規化のための文の長さの確率である.次のステップは,日本語の単語
は,正規化のための文の長さの確率である.次のステップは,日本語の単語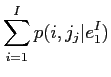
![$\displaystyle Pr(j^{J}_{1}\vert e^{I}_{1}) = p(J\vert I)\cdot \prod^{J}_{j=1}\sum^{I}_{i=1}[p(i\vert j,I)\cdot p(j_{j}\vert e_{i})]$](img87.png)
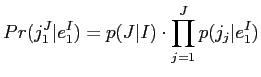
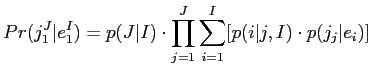
![$ [j^{j_{s}}_{1};e^{I_{s}}_{1}],s = 1, ..., S$](img91.png) からなる対訳コーパスを使用する.最大尤度基準を使用して,以下の反復方程式を得る.
からなる対訳コーパスを使用する.最大尤度基準を使用して,以下の反復方程式を得る.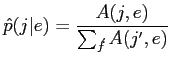
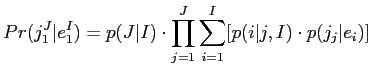 が使用される.したがって,アライメント確率の特定のモデルが使用される.
が使用される.したがって,アライメント確率の特定のモデルが使用される.
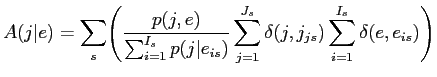
![$\displaystyle Pr(j^{J}_{1}\vert e^{I}_{1}) \cong \prod^{J}_{j=1} \underset{i}{\mathrm{max}} [p(i\vert j,I)\cdot p(j_{j}\vert e_{i})]$](img95.png)
![]() の単語
の単語![]() を位置
を位置
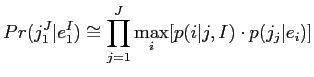 の
の![]() に割り当てる写像
に割り当てる写像![]() を導入する.位置
を導入する.位置![]() に対するアライメント
に対するアライメント![]() の確率は,前のアラインメント
の確率は,前のアラインメント![]() に依存する.
に依存する.
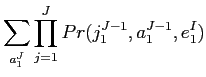
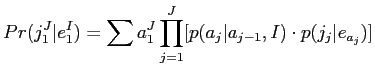 または
または
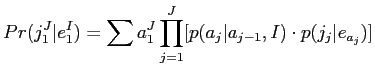 はジャンプ幅
はジャンプ幅
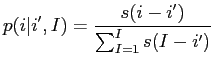 に対して,HMMアライメント確率が正規化制約を満たすことを保証する.混合モデルは一次HMMとは対照的に,ゼロ次モデルとして解釈できる.IBM Model2と同様に,ここでも最大近似を使用する.
に対して,HMMアライメント確率が正規化制約を満たすことを保証する.混合モデルは一次HMMとは対照的に,ゼロ次モデルとして解釈できる.IBM Model2と同様に,ここでも最大近似を使用する.
![$\displaystyle Q(i,j) = p(j_j\vert e_{i}) \underset{i=1,...,I}{\mathrm{max}}[p(i\vert i^{\prime},I)\cdot Q(i^{\prime},J - 1)]$](img117.png)