| (2.10) |
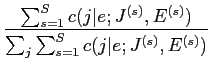 ,
日本語文の長さ
,
日本語文の長さ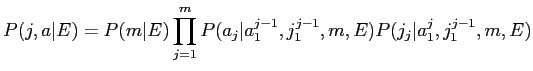 に依存するとし,以下の式で表す.
に依存するとし,以下の式で表す.
| (2.10) |
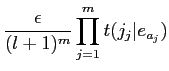 |
(2.11) | ||
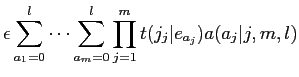 |
(2.12) |
Model2において,対訳文中の英単語![]() と日単語
と日単語![]() が対応付けされる回数の期待値である
が対応付けされる回数の期待値である
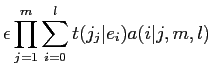 と,日単語の位置
と,日単語の位置![]() と英単語の位置
と英単語の位置![]() が対応付けられる回数の期待値
が対応付けられる回数の期待値
![]() が存在する.以下に,期待値
が存在する.以下に,期待値
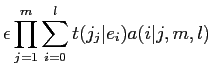 と
と
![]() を求める式を示す.
を求める式を示す.
| (2.13) | |||
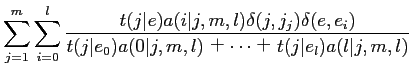 |
(2.14) |
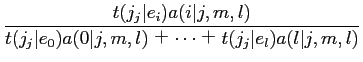 が挙げられるが,これはModel1として考えることができる.また,最適解が保証されているModel1で求められた値を初期値として用いることで,最適解を求めることができる.
が挙げられるが,これはModel1として考えることができる.また,最適解が保証されているModel1で求められた値を初期値として用いることで,最適解を求めることができる.