


Next: 提案手法2(Dice係数と類似度の積())を使用する手法
Up: 提案手法
Previous: 概要
目次
提案手法1はフレーズ確率の総積(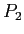 )を用いる手法である.
フレーズ確率の総積
)を用いる手法である.
フレーズ確率の総積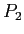 は同一パターンの変数部のフレーズ確率
は同一パターンの変数部のフレーズ確率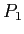 の総積である.
計算式を式3.1に示す.
の総積である.
計算式を式3.1に示す.
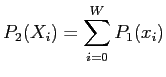 |
|
|
(3.1) |
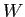 ;変数の数
;変数の数
以下に例を示す.表3.1に対訳句作成時に使用するデータの具体例を示す.
表3.1の対訳学習文は対訳句作成に用いる文である.
対訳文パターンは対訳句作成に用いるパターンである.
対訳句作成の手順を以下に示す.
- 手順1
- 対訳学習文とパターンを照合
- 手順2
- 単語レベル文パターンの変数部に対応する組み合わせの対訳句をすべて抽出
表3.2に抽出した対訳句の具体例を示す.
- 手順3
- 式を用いて対訳句にフレーズ確率を付与
表3.2に示しているフレーズ確率は対数値である.フレーズ確率の総積はパターンにおける変数部のフレーズ確率の総積である.
ここで,フレーズ確率の総積は1つの変数の組から作成された対訳句において同じ値となる.
表3.2におけるフレーズ確率の総積の計算式を式3.2に示す.
最終的なフレーズ確率の総積は全てのパターンと対訳文におけるフレーズ確率の総積の再良値となる.
2018-03-06