


�$B HMM parameter estimation
�$B>e$X�(B: Solution Method using Ergodic
�$BLa$k�(B: Solution Method using Ergodic
When the number of categories 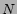 is known and segmentation boundaries are
unknown, it is possible to apply the Ergodic HMM. In this case, one can
consider that 'category' corresponds to 'state' and the signal
sequence corresponds to the symbol generated from the state. The
problem divides into the following two problems.
is known and segmentation boundaries are
unknown, it is possible to apply the Ergodic HMM. In this case, one can
consider that 'category' corresponds to 'state' and the signal
sequence corresponds to the symbol generated from the state. The
problem divides into the following two problems.
- The problem of estimating the HMM parameter
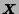 that maximizes the
likelihood of the signal sequence. Parameter
that maximizes the
likelihood of the signal sequence. Parameter
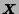 consists of the
initial state probability
consists of the
initial state probability
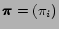 , the state transition
probability
, the state transition
probability
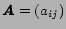 and the symbol output probability
and the symbol output probability
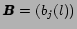 .
.
- The problem of estimating the state transition sequence that generate the highest probability of outputting the
signal sequence
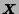 for the HMM parameter
for the HMM parameter
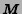 (estimate of optimal state sequence).
(estimate of optimal state sequence).
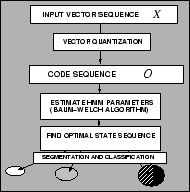
Fig.2 outlines our solution.
�$B?^�(B 2:
Flow chart that includes an Ergodic HMM for the 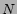 -signal source problem
-signal source problem
 |
Jin'ichi Murakami
�$BJ?@.�(B13�$BG/�(B1�$B7n�(B19�$BF|�(B
![]() is known and segmentation boundaries are
unknown, it is possible to apply the Ergodic HMM. In this case, one can
consider that 'category' corresponds to 'state' and the signal
sequence corresponds to the symbol generated from the state. The
problem divides into the following two problems.
is known and segmentation boundaries are
unknown, it is possible to apply the Ergodic HMM. In this case, one can
consider that 'category' corresponds to 'state' and the signal
sequence corresponds to the symbol generated from the state. The
problem divides into the following two problems.