Next: Attentionモデル Up: Encoder-Decoderモデル Previous: Encoder-Decoderモデル 目次
ここで![]() は各時刻tの隠れ層の状態であり, cは隠れ層を用いて生成されたベクトルである.
fおよびqは活性化関数であり,
Sutskeverら[5]
はfにLSTMを用いた上,
は各時刻tの隠れ層の状態であり, cは隠れ層を用いて生成されたベクトルである.
fおよびqは活性化関数であり,
Sutskeverら[5]
はfにLSTMを用いた上,
![]() としている.
Decoderは文脈ベクトルcと既に生成された単語
としている.
Decoderは文脈ベクトルcと既に生成された単語
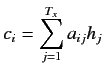 が与えられた際の次の単語
が与えられた際の次の単語![]() を予測するように訓練され, 結合確率を
2.34式に示す条件式に分解することで翻訳文
を予測するように訓練され, 結合確率を
2.34式に示す条件式に分解することで翻訳文
![]() を得る条件付き確率を定義している.
を得る条件付き確率を定義している.
2.33式および2.34式で表されるRNNを用いて, それぞれの条件付き確率は
2.35式によりモデル化される.
ここで, gは非線形の多層関数であり, ![]() の確率を生成する.
の確率を生成する. はRNNの隠れ層となる.
はRNNの隠れ層となる.