Ňż∑◊ň›Őű§«§ŌľÁ§ň
| (2.23) | |
| (2.24) |
ľ¬ļ›§ő∑◊ĽĽő„§Ú(2.24)§ňľ®§Ļ.
| (2.25) | |
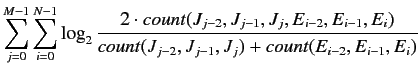 |
(2.26) |
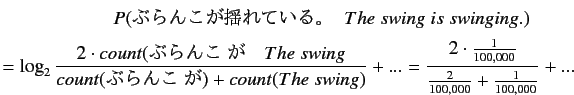 |
(2.27) |
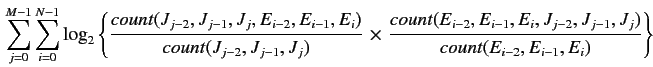 |
(2.28) |
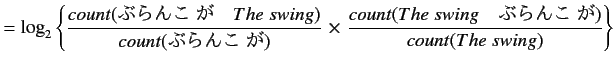 |
(2.29) |
| (2.30) |
ň‹ł¶Ķś§«§Ō, łņłž•‚•«•Ž§ňTri-gram§ő¬Ś§Ô§Í§ň High order Joint Probability§ÚĽ»Õ—§Ļ§Ž. High order Joint Probability§Úľį2.25§ňľ®§Ļ.
 |
(2.31) |
| (2.32) |
ľ¬ļ›§ő∑◊ĽĽő„§Ú(2.26)§ňľ®§Ļ.§ř§Ņ, ∑◊ĽĽľį§¨ńĻ§Į§ňĶŕ§÷§Ņ§Š, ¬Ť1Ļŗ§ő§Ŗ∑◊ĽĽő„§Úľ®§Ļ.
| (2.33) | |
| (2.34) | |
 |
(2.35) |
 |
(2.36) |
ľ¬ļ›§ő∑◊ĽĽő„§Ú(2.28)§ňľ®§Ļ.§ř§Ņ, ∑◊ĽĽľį§¨ńĻ§Į§ňĶŕ§÷§Ņ§Š, ¬Ť1Ļŗ§ő§Ŗ∑◊ĽĽő„§Úľ®§Ļ.
ľ¬ļ›§ő∑◊ĽĽő„§Ú(2.30)§ňľ®§Ļ.§ř§Ņ, ∑◊ĽĽľį§¨ńĻ§Į§ňĶŕ§÷§Ņ§Š, ¬Ť1Ļŗ§ő§Ŗ∑◊ĽĽő„§Úľ®§Ļ.
| (2.40) | |
 |
(2.41) |
 |
(2.42) |


