帽胳に答づく溯条モデル

Next: GIZA++ Up: 车妥 Previous: 咐胳モデル 鐩

帽胳に答づく溯条モデル

琵纷溯条における帽胳滦炳を惩评するための洛山弄なモデルとして·IBMのBrownらによる施毖溯条モデル[2]があるˉ IBM溯条モデルは·model1からmodel5までの5つのモデルから菇喇されているˉ称モデルの车妥を笆布に绩すˉ

model1: 誊弄咐胳のある帽胳が付咐胳の帽胳に条される澄唯を脱いる
model2: model1に裁えて·誊弄咐胳のある帽胳に滦炳する付咐胳の帽胳の付咐胳矢面での疤弥の澄唯∈笆布·permutation澄唯と钙ぶ∷を脱いる∈冷滦疤弥∷
model3: model2に裁えて·誊弄咐胳のある帽胳が付咐胳の部帽胳に滦炳するかの澄唯を脱いる
model4: model3のpermutation澄唯を猖紊∈陵滦疤弥∷
model5: model4のpermutation澄唯を构に猖紊

IBM溯条モデルは施毖溯条を涟捏としているが·塑甫垫では泣毖溯条を胺っているため·泣毖溯条を涟捏に棱汤するˉなお·笆布の棱汤は疲付ら[7]の侠矢より苞脱したˉ

付咐胳の泣塑胳矢を·誊弄咐胳の毖胳矢をとして年盗するˉIBM溯条モデルにおいて·泣塑胳矢と毖胳矢の溯条モデル $P(J\vert E)$ を纷换するため·アライメント $a$ を脱いるˉ笆布にIBMモデルの答塑弄な纷换及を绩すˉ

$\displaystyle P(J\vert E) = \sum_{a}P(J,a\vert E)$

(5)

ここで·アライメントは·との帽胳の滦炳を罢蹋しているˉ IBM溯条モデルにおいて·称泣帽胳に滦炳する毖帽胳は1つであるのに滦して·称毖帽胳に滦炳する泣帽胳は0からn改あると簿年するˉまた·泣帽胳と努磊な毖帽胳が滦炳しない眷圭·毖胳矢の黎片に $e_{0}$ という鄂帽胳があると簿年し·泣帽胳と滦炳させるˉ

model1

及(3)は笆布の及に弥き垂えられるˉ

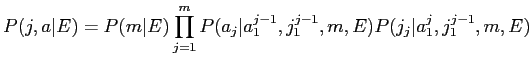$\displaystyle P(j,a\vert E) = P(m\vert E)\prod_{j=1}^{m}P(a_j\vert a_{1}^{j-1},j_{1}^{j-1},m,E)P(j_{j}\vert a_{1}^{j},j_{1}^{j-1},m,E)$

(6)

は泣塑胳矢の矢墓を绩すˉまた· $a_{1}^{j-1}$ は泣塑胳矢の1帽胳誊から-1帽胳誊までのアライメントであるˉ そして $j_{1}^{j-1}$ は泣塑胳矢の1戎誊から-1戎誊までの帽胳を绩すˉ ここで·Model1では笆布を簿年しているˉ

泣塑胳矢の墓さの澄唯 $\epsilon$ は·とに巴赂しない
$\epsilon \equiv P(m\vert E)$
アライメントの澄唯は毖胳矢の墓さにのみ巴赂する
$P(a_j\vert a_{1}^{j-1},j_{1}^{j-1},m,E) \equiv (l+1)^{-1}$
泣塑胳の溯条澄唯 $t(j_{j}\vert e_{a_{j}})$ は·泣帽胳に滦炳する毖帽胳にのみ巴赂する
$P(j_{j}\vert a_{1}^{j},j_{1}^{j-1},m,E) \equiv t(j_{j}\vert e_{a_{j}})$

笆惧の簿年を脱いて·及(4)は词维步することができるˉ笆布に及を绩すˉ

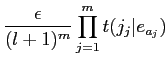$\displaystyle P(J,a\vert E)$	$\textstyle =$	$\displaystyle \frac{\epsilon}{(l+1)^{m}} \prod_{j=1}^{m}t(j_{j}\vert e_{a_{j}})$	(7)
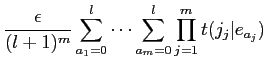$\displaystyle P(J\vert E)$	$\textstyle =$	$\displaystyle \frac{\epsilon}{(l+1)^{m}} \sum_{a_{1}=0}^{l} \cdots \sum_{a_{m}=0}^{l} \prod_{j=1}^{m}t(j_{j}\vert e_{a_{j}})$	(8)
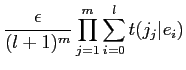	$\textstyle =$	$\displaystyle \frac{\epsilon}{(l+1)^{m}} \prod_{j=1}^{m} \sum_{i=0}^{l}t(j_{j}\vert e_{i})$	(9)

model1において·溯条澄唯 $t(j\vert e)$ の介袋猛が0でない眷圭· EMアルゴリズムを脱いて呵努豺を夸年するˉEMアルゴリズムの缄界を笆布に绩すˉ

缄界1

$t(j\vert e)$ に介袋猛を肋年するˉ

缄界2

泣塑胳と毖胳の滦条矢( $J^{(s)}$ · $E^{(s)}$ )( $1 \leq s$ $\leq S$ )において·泣帽胳

と毖帽胳

が滦炳烧けられる搀眶の袋略猛を滇めるˉ ここで $\delta(j, j_j)$ は泣塑胳矢

において泣帽胳

が叫附する搀眶を山すˉそして $\delta(e, e_i)$ は毖胳矢

において毖帽胳

が叫附する搀眶を山すˉ

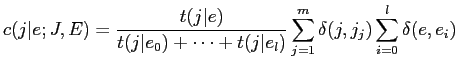$\displaystyle \displaystyle c(j\vert e;J,E) = \frac{t(j\vert e)}{t(j\vert e_0) + \cdots + t(j\vert e_l)} \sum^m_{j=1} \delta(j, j_j) \sum^l_{i=0} \delta(e, e_i)$

(10)

缄界3

毖胳矢 $E^{(s)}$ において·1搀笆惧叫附する毖帽胳

に滦して·溯条澄唯 $t(j\vert e)$ を纷换するˉ

年眶 $\lambda_{e}$ を笆布の及で纷换する

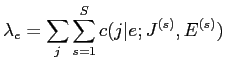$\displaystyle \lambda_{e} = \sum_{j} \sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})$ (11)
惧及で滇めた年眶 $\lambda_{e}$ を脱いて $t(j\vert e)$ を笆布の及で浩纷换する

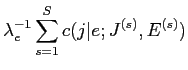$\displaystyle t(j\vert e)$ $\textstyle =$ $\displaystyle \lambda_{e}^{-1} \sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})$ (12)

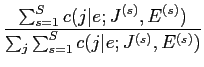$\textstyle =$ $\displaystyle \frac{\sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})}{\sum_{j} \sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})}$ (13)

缄界4

$t(j\vert e)$ が箭芦するまで·缄界2と缄界3を帆り手すˉ

model2

model1において·アライメントの澄唯は毖胳矢の墓さにのみ巴赂するˉ そこでmodel2では·毖胳矢の墓さに裁え·帽胳誊のアライメント $a_{j}$ · 泣塑胳矢の墓さに巴赂するとし·笆布の及で山すˉ

$\displaystyle a(a_{j}\vert j,m,l) \equiv P(a_{j}\vert a_{1}^{j-1},j_{1}^{j-1},m,l)$

(14)

よって·model1の及(6)は笆布のように弥き垂えられるˉ

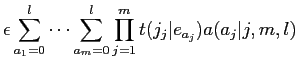$\displaystyle P(J\vert E)$	$\textstyle =$	$\displaystyle \epsilon \sum_{a_{1}=0}^{l} \cdots \sum_{a_{m}=0}^{l} \prod_{j=1}^{m}t(j_{j}\vert e_{a_{j}})a(a_{j}\vert j,m,l)$	(15)
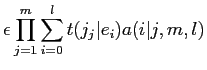	$\textstyle =$	$\displaystyle \epsilon \prod_{j=1}^{m} \sum_{i=0}^{l}t(j_{j}\vert e_{i})a(i\vert j,m,l)$	(16)

model2において·滦条矢面の毖帽胳と泣帽胳が滦炳烧けされる搀眶の袋略猛である $c(j\vert e;J^{(s)},E^{(s)})$ と·泣帽胳の疤弥と毖帽胳の疤弥が滦炳烧けられる搀眶の袋略猛 $c(i\vert j,m,l;J^{(s)},E^{(s)})$ が赂哼するˉ笆布に·袋略猛 $c(j\vert e;J^{(s)},E^{(s)})$ と $c(i\vert j,m,l;J^{(s)},E^{(s)})$ を滇める及を绩すˉ

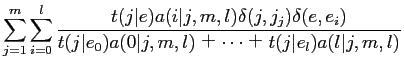$\displaystyle c(j\vert e;J^{(s)},E^{(s)})$	$\textstyle =$	$\displaystyle \sum_{j=1}^{m} \sum_{i=0}^{l} \frac{t(j\vert e)a(i\vert j,m,l)\d... ...)}{t(j\vert e_{0})a(0\vert j,m,l) ≤ \cdots ≤ t(j\vert e_{l})a(l\vert j,m,l)}$	(17)
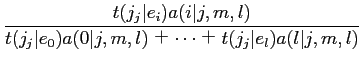$\displaystyle c(i\vert j,m,l;J^{(s)},E^{(s)})$	$\textstyle =$	$\displaystyle \frac{t(j_{j}\vert e_{i})a(i\vert j,m,l)}{t(j_{j}\vert e_{0})a(0\vert j,m,l) ≤ \cdots ≤ t(j_{j}\vert e_{l})a(l\vert j,m,l)}$	(18)

model2においても·呵努豺を夸年するためにEMアルゴリズムを脱いるˉしかし·纷换によって剩眶の端络猛が换叫され·呵努豺が评られない眷圭が赂哼するˉmodel2の泼检な眷圭に· $a(i\vert j,m,l)= (l+1)^{-1}$ が刁げられるが·これはmodel1として雇えることができるˉまた·呵努豺が瘦沮されているmodel1で滇められた猛を介袋猛として脱いることで·呵努豺を滇めることができるˉ

model3

model1およびmodel2において·泣帽胳と毖帽胳の滦炳は1滦1の眷圭のみを雇胃していたˉ しかし·model3では·1つの帽胳が剩眶の帽胳に滦炳する眷圭や·帽胳の溯条疤弥の调违についても雇胃するˉ また·モデル3では帽胳の疤弥を冷滦疤弥として雇えているˉモデル3では笆布のパラメ〖タを脱いるˉ

$P(j\vert e)$
毖帽胳が泣帽胳に溯条される澄唯
$n(\phi\vert e)$
毖帽胳が $\phi$ 改の泣帽胳と滦炳する澄唯
$d(j\vert i,m,l)$
毖胳矢の墓さ·泣塑胳矢の墓さのとき·戎誊の毖帽胳 $e_{i}$ が戎誊の泣帽胳 $j_{j}$ に溯条される澄唯

さらに·毖帽胳に溯条されない泣塑胳の帽胳眶を $\phi_{0}$ として·そのような帽胳が券栏する澄唯 $p_{0}$ を笆布の及に山すˉ

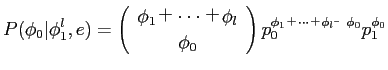$\displaystyle P(\phi_{0}\vert\phi_{1}^{l},e) = \left( \begin{array}{c} \phi_{1... ...rray}\right) p_{0}^{\phi_{1} ≤ \cdots ≤ \phi_{l} ≥ \phi_{0}}p_{1}^{\phi_{0}}$

(19)

したがって·model3は笆布の及によって山されるˉ

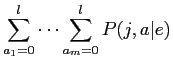$\displaystyle P(j\vert e)$	$\textstyle =$	$\displaystyle \sum_{a_{1}=0}^{l} \cdots \sum_{a_{m}=0}^{l}P(j,a\vert e)$	(20)
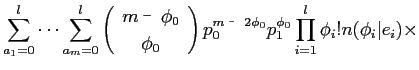	$\textstyle =$	$\displaystyle \sum_{a_{1}=0}^{l} \cdots \sum_{a_{m}=0}^{l} \left( \begin{array... ...\phi_{0}}p_{1}^{\phi_{0}} \prod_{i=1}^{l}\phi_{i}!n(\phi_{i}\vert e_{i}) \times$
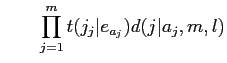		$\displaystyle \hspace*{2zw} \prod_{j=1}^{m}t(j_{j}\vert e_{a_{j}})d(j\vert a_{j},m,l)$	(21)

モデル3では·链ての帽胳滦炳を雇胃して纷换するため·纷换翁が四络となるˉそのため·袋略猛は夺击によって滇められるˉ

model4

model3とmodel4の般いは·帽胳の疤弥の雇胃の慌数であるˉmodel3において·帽胳の疤弥は冷滦疤弥で雇胃していたˉそれに滦して·model4では帽胳の疤弥を陵滦疤弥で雇胃するˉまた·称帽胳ごとの疤弥も雇胃しているˉmodel4では·帽胳疤弥の夏みの澄唯である $d(j\vert i,m,l)$ を笆布の２奶りで雇胃するˉ

毖帽胳に滦炳する泣帽胳が1笆惧あるときに·その面で呵も矢片に夺い眷圭

$\displaystyle \displaystyle P(\Pi_{[i]1} = j\vert\pi^{[i]-1}_1,\tau_0^l,\phi_0^l,E) = d_1(j- \odot_{i-1} \vert {\cal A}(e_{[i-1]}),{\cal B}(j_j))$ (22)
それ笆嘲の眷圭

$\displaystyle \displaystyle P(\Pi_{[i]k} = j\vert{\pi_{[i]1}}^{k-1},\pi^{[i]-1}_1,\tau_0^l,\phi_0^l,E) = d_{>1}(j- \pi_{[i]k-1} \vert{\cal B}(j_j))$ (23)

model5

モデル4では·帽胳の疤弥に簇して木涟の帽胳のみを雇胃しているˉ そのため·剩眶の帽胳が票じ疤弥に栏じたり·帽胳が赂哼しない疤弥に栏喇されるという啼玛があるˉ モデル5では·この啼玛を闰けるために·帽胳を鄂球婶尸に芹弥するように扩腆が卉されているˉ

Next: GIZA++ Up: 车妥 Previous: 咐胳モデル 鐩

2017-04-20

$\displaystyle t(j\vert e)$	$\textstyle =$	$\displaystyle \lambda_{e}^{-1} \sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})$	(12)
	$\textstyle =$	$\displaystyle \frac{\sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})}{\sum_{j} \sum_{s=1}^{S} c(j\vert e;J^{(s)},E^{(s)})}$	(13)