本演習を実施するにあたり、言語の選択をやり直して下さい。
使用する言語: Pretty Big
メニューバーから次のとおりクリックする。「言語」→「言語の選択」→「(レガシーな言語)Pretty Big」
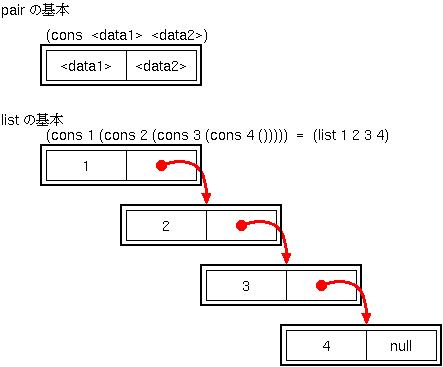
ペアとは2つのデータをまとめた構造体のことである。ドットペアと呼ばれることもある。
ペアに対する基本操作は以下の3つである:
| 意味 | 関数名 | 形式 |
|---|---|---|
| ペアの作成 | cons | (cons 〈データ1〉 〈データ2〉) |
| ペアの左側の抽出 | car | (car 〈ペア〉) |
| ペアの右側の抽出 | cdr | (cdr 〈ペア〉) |
以下を定義エリア(Definitions)に記述し、実行(Run)してみよう。
(define p1 (cons 100 200)) (car p1) (cdr p1) |
C言語の演習などでもお馴染の「片方向の線形リスト」は、schemeではペアを組合せて作成する。
たとえば、次のようにペアを使うと、数字のリストになる。
(define p2 (cons 1 (cons 2 (cons 3 (cons 4 ()))))) |
ここで、() は空のリストを表す。
このように、リストをペアの集りで定義できるが、分りにくい。そこで、次のように書くことができる。
(define p3 (list 1 2 3 4)) または (define p3 '(1 2 3 4)) |
演習では印刷上のわかりやすさから、クオートの表記はせず、list の表記を用いる。

equal? を使って p2 と p3 が等しいことを確認しよう。#t が返り値となるはずである。
> (equal? p2 p3) |
1つのリストに対する基本操作を以下にまとめる:
| 意味 | 関数名 | 形式 |
|---|---|---|
| リストの作成 | list | (list 〈データ1〉 〈データ2〉 … 〈データn〉) |
| リストの先頭に要素を追加 | cons | (cons 〈要素〉 〈リスト〉) |
| リストから先頭要素を抽出 | car | (car 〈リスト〉) |
| リストから2番目以降のリストを抽出 | cdr | (cdr 〈リスト〉) |
| リストが空かどうかの検査 | null? | (null? 〈リスト〉) |
幾つかリスト操作を確認しよう。
> (list 1 2 3) > (cons 1 (list 5 4 3)) > (car (list 1 2 3)) > (cdr (list 1 2 3)) > (null? (list 1 2 3)) > (null? (list )) > (cdr (list 1)) > (null? (cdr (list 1))) ※ この方法で、リストの要素数が1つかどうかの検査が可能 > (define x (list 1 2 3)) ※ 名前を付けることができる > (car x) > (cdr x) |
リストを操作するプログラムの多くは、再帰呼び出しを使う。簡単なものから練習しよう。
数を要素とするリストを入力とし、その合計値を返す関数 sum を作成せよ。
(解答例)次の順番で考えるとよい。
(define sum
(lambda (lst)
; ここにもっと書き込む予定 ... (イ)
))
|
(if (null? lst)
; ここに、空リストのときの処理を書き込む予定 ... (ロ)
; ここに、リストに要素が残っているときの処理を書き込む予定 ) ... (ハ)
|
0 ; (∵ 空リストの合計値は 0)
|
(+ リストlstの先頭の要素 リストlstの2番目以降の要素列、すなわちリストの合計値)
|
ここで、リストlstの先頭の要素は、(car lst) で得られ、
リストlstの2番目以降の要素列は、(cdr lst) で得られる。
(cdr lst) の合計値は、(sum (cdr lst)) である。
したがって、(ハ)には、以下のように書き込む。
(+ (car lst) (sum (cdr lst)))
|
(1) 数を要素とするリストを入力とし、各要素を2乗して、その合計値を返す関数 sum2 を作成せよ。
(2) リストの要素数を数える関数 size を作成せよ。例えば (list 1 2 3 'ok 'ng) を入力すると 5 を返す。
(1) 数を要素とするリストを入力とし、各要素を2乗したリストを返す関数 pow2-list を作成せよ。例えば (list 1 2 3 4) を入力すると (list 1 4 9 16) を返す。
(2) 数を要素とするリストと数 d を入力とし、リストの各要素について d で割った余りを求める関数 mod-list を作成せよ。例えば (list 1 2 3 4 5 6 7) と 3 を入力すると (list 1 2 0 1 2 0 1) を返す。なお、modulo により余りを計算できる。
(1) 2つのリスト lst1、lst2 を入力とし、lst1 の後に lst2 を接続したリストを返す関数 cat-list を作成せよ。例えば (list 1 2 3) と (list 4 5 6) を入力すると (list 1 2 3 4 5 6) を返す。
(2) 2つのリスト lst1、lst2 を入力とし、リストの要素を交互に要素とするリストを返す関数 merge-list を作成せよ。例えば (list 1 2 3) と (list 4 5 6) を入力すると (list 1 4 2 5 3 6) を返す。また、(list 1 2 3) と (list 4 5 6 7 8 9) を入力すると (list 1 4 2 5 3 6 7 8 9) を返す。
再帰関数は、再帰計算の結果に何か計算をして返り値とする場合と、再帰計算の結果をそのまま返り値とする場合とに分けられる。
前者は、上記の例題で紹介したとおりである。すなわち、(+ (car lst) (sum (cdr lst))) という計算は、(sum (cdr lst)) という再帰呼出しの結果を足し算に使用しており、その結果が返り値となっている。
後者は、末尾再帰関数と呼ばれる。数のリストの合計値を求める関数の例を以下に示す。
*** 解1 ***
(define sum00
(lambda (lst n)
(if (null? lst)
n
(sum00 (cdr lst) (+ n (car lst))))))
(define sum
(lambda (lst)
(sum00 lst 0)))
|
sum00 は、数のリスト lst と、これまでの合計値 n を入力とする。例えば、(list 1 2 3 4) を計算する場合、再帰呼出しの様子は次のようになる。
最初:(sum00 (list 1 2 3 4) 0)
再帰1: (sum00 (list 2 3 4) 1)
再帰2: (sum00 (list 3 4) 3)
再帰3: (sum00 (list 4) 6)
再帰4: (sum00 () 10)
なお、sum00 を sum のlambda 式の中に閉じ込めることができる。
*** 解2 ***
(define sum
(lambda (lst)
(define sum00
(lambda (lst n)
(if (null? lst)
n
(sum00 (cdr lst) (+ n (car lst))))))
(sum00 lst 0)))
|
リスト操作と再帰呼出しに慣れるために、以下の関数を作ろう。
(1) 数のリストを入力とし、最大値を返す関数 max-list
(2) 数のリストを入力とし、分散を返す関数 variancce-list
(3) 確率値のリストを入力とし、エントロピーを返す関数 entropy(ヒント:エントロピーは、-Σipi log2 pi である)
(4) 数のリストを入力とし、偶数値だけのリストを作って返す関数 even-list(ヒント:数値が偶数であることを判定する関数 even? は既に存在する。例、(even? 4) ⇒ #t)
(5) 長さの同じ2つの数のリストを入力とし、同じ番目の数の和を要素とするリストを返す関数 add-list(例、(add-list (list 1 2 3) (list 4 5 6)) の返り値は (list 5 7 9)である。)
(6) リストを入力とし、その順序を逆にしたリストを作って返す関数 rev-list(例、(rev-list (list 1 2 3 4)) の返り値は (list 4 3 2 1) である。)