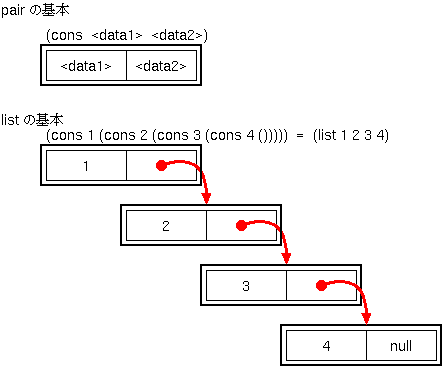
ペアとは2つのデータをまとめた構造体のことである。ドットペアと呼ばれることもある。
ペアに対する基本操作は以下の3つである:
| 意味 | 関数名 | 形式 |
|---|---|---|
| ペアの作成 | cons | (cons 〈データ1〉 〈データ2〉) |
| ペアの左側の抽出 | car | (car 〈ペア〉) |
| ペアの右側の抽出 | cdr | (cdr 〈ペア〉) |
以下を Definitions に記述し、Run してみよう。
(define p1 (cons 100 200)) (car p1) (cdr p1) |
ペアを組み合わせて、データを並べた構造体をリストと呼ぶ。
たとえば、次のようにペアを使うと、数字のリストになる。
(define p2 (cons 1 (cons 2 (cons 3 (cons 4 ()))))) |
() は空を表す
このように、リストの正体は、ペアの集りであるが、分りにくい。そこで、次のように書くことができる。
(define p3 (list 1 2 3 4)) または (define p3 '(1 2 3 4)) |
演習では印刷上のわかりやすさから、クオートの表記はせず、list の表記を用いる。

equal? を使って p2 と p3 が等しいことを確認しよう。
> (equal? p2 p3) |
リストに対する基本操作を以下にまとめる:
| 意味 | 関数名 | 形式 |
|---|---|---|
| リストの作成 | list | (list 〈データ1〉 〈データ2〉 … 〈データn〉) |
| リストの先頭に要素を追加 | cons | (cons 〈要素〉 〈リスト〉) |
| リストから先頭要素を抽出 | car | (car 〈リスト〉) |
| リストから2番目以降のリストを抽出 | cdr | (cdr 〈リスト〉) |
| リストが空かどうかの検査 | null? | (null? 〈リスト〉) |
幾つかリスト操作を確認しよう。
> (list 1 2 3) > (cons 1 (list 5 4 3)) > (car (list 1 2 3)) > (cdr (list 1 2 3)) > (null? (list 1 2 3)) > (null? (list )) > (cdr (list 1)) > (null? (cdr (list 1))) ※ この方法で、リストの要素数が1つかどうかの検査が可能 > (define x (list 1 2 3)) ※ 名前を付けることができる > (car x) > (cdr x) |
よく使う組み込みの関数
下記の動作を確認しよう。
> (length (list 1 2 3 4 5)) > (append (list 1 2 3) (list 4 5 6)) |
リストを扱う関数を作ってみよう。
実行方法: (list-sum (list 1 2 3 4 5))
予想結果: 15
簡単な解答例:
*** 解1 ***
(define list-sum
(lambda (lst)
(if (null? lst)
0
(+ (car lst) (list-sum (cdr lst))))))
|
末尾再帰関数として作る場合:
*** 解2 ***
(define list-sum2
(lambda (lst n)
(if (null? lst)
n
(list-sum2 (cdr lst) (+ n (car lst))))))
(define list-sum
(lambda (lst)
(list-sum2 lst 0)))
|
解2を変更して、関数定義を内部に持たせる場合:
*** 解3 ***
(define list-sum
(lambda (lst)
(define list-sum2
(lambda (lst n)
(if (null? lst)
n
(list-sum2 (cdr lst) (+ n (car lst))))))
(list-sum2 lst 0)))
|
※ 解2は、Interactions 上で list-sum2 を実行することができるが、解3は、実行できない。
実行方法: (list-max (list 1 2 4 5 3))
予想結果: 5
簡単だけど愚かな解答例:
*** 解1 ***
(define list-max
(lambda (lst)
(if (null? (cdr lst)) 要素数が1つか?
(car lst) 先頭要素を返す
(if (> (car lst) (list-max (cdr lst)) 先頭要素と2番目以降の最大値を比較
(car lst) 先頭要素を返す
(list-max (cdr lst)))))) 2番目以降の最大値を返す
|
2つめの if 文で、list-max の計算をするが、もし、その値のほうが大きいとき、2つ下の式が評価されるのだが、再び同じ計算をすることになる。
無駄な計算を省いた解答例:
*** 解2 ***
(define greater
(lambda (m n)
(if (> m n) m n)))
(define list-max
(lambda (lst)
(if (null? (cdr lst))
(car lst)
(greater (car lst) (list-max (cdr lst))))))
|
最後の行で、リストの2番目以降の最大値を、まず求めており、その結果が greater で使われているので、同じ計算を繰り返すことはない。
一方、末尾再帰関数として作成してみると、もっと簡単になる。
*** 解3 ***
(define list-max2
(lambda (lst n) これから計算すべきリスト lst、これまでの最大値 n
(if (null? lst) リストが空のとき、
n これまでの最大値 n が全体の最大値
(if (> n (car lst)) そうでなければ、先頭要素とこれまでの最大値を比較
(list-max2 (cdr lst) n) n が大きいとき
(list-max2 (cdr lst) (car lst)))))) 先頭要素が大きいとき
(define list-max
(lambda (lst)
(list-max2 (cdr lst) (car lst))))
先頭要素をこれまでの最大値とし、2番目以降を処理
|
list-max2 の定義を内部に持たせる場合:
*** 解4 ***
(define list-max
(lambda (lst)
(define list-max2
(lambda (lst n)
(if (null? lst)
n
(if (> n (car lst))
(list-max2 (cdr lst) n)
(list-max2 (cdr lst) (car lst))))))
(list-max2 (cdr lst) (car lst))))
|
例題2では、リストから値を抽出する関数であった。次にリストを返す関数を作ってみよう。
実行方法: (my-append (list 1 2 3) (list 4 5 6))
予想結果: (1 2 3 4 5 6)
(define my-append
(lambda (lst1 lst2)
(if (null? lst1)
lst2
(cons (car lst1) (my-append (cdr lst1) lst2)))))
|
※ append は、末尾再帰関数が簡単には作れません。
実行方法: (replace-sanbai (list 1 2 3 4 5 6 7 8 9 10))
予想結果: (1 2 '* 4 5 '* 7 8 '* 10)
(define replace-sanbai
(lambda (lst)
(if (null? lst)
(list) ← 空のリスト
(if (= (modulo (car lst) 3) 0)
(cons '* (replace-sanbai (cdr lst)))
(cons (car lst) (replace-sanbai (cdr lst)))))))
|
実行方法: (list-double (list 1 2 3 4 5))
予想結果: (2 4 6 8 10)
(define list-double
(lambda (lst)
(if (null? lst)
(list) ← 空のリスト
(cons (* 2 (car lst)) (list-double (cdr lst))))))
|
リスト操作と再帰呼出しに慣れるために、以下の関数を作ろう。
よく使うプリンタの用紙は、A4サイズである(210mm x 297mm)。この用紙は、長辺を半分に折るとA5サイズの用紙になる(小数点の切り捨てはtruncate関数を使用)。A0サイズは、841mm x 1189mm という大きさである。では、nを変数として Anサイズの2辺の長さをペアの値で返す関数 (paper-a-size n) を定義せよ。
動作例:(paper-a-size 4) ⇒ (210 . 297)
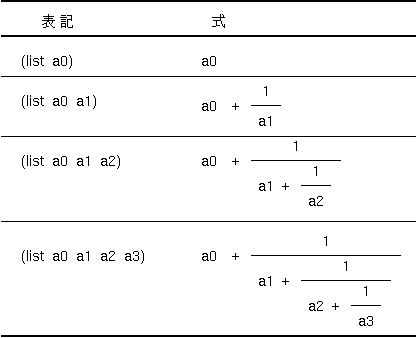
表1には連分数の表記とその具体的な式の関係が示されている。たとえば、(list 2 4)は、2 + 1 / 4 という式の略記であり、(list 3 6 9) は、3 + 1 / (6 + 1 / 9) という式の略記である。そこで、入力される数のリストに対して連分数を計算する関数 contfrac を定義せよ。
表1 連分数の表記と計算式