第7回制御構造（5月29日）

今日の課題

lambda と順接
「条件式」の評価
再帰

■ lambda 式（ラムダ式）

関数を定義する

lambda 式は、特殊形式の式である。lambda を使うと、関数を定義することができる。

(lambda (引数1 引数2 … 引数n) 式1 式2 … 式m)

たとえば、「引数の値を、３倍して、返す」という関数は、lambda 式を使うと、次のように表わされる。

> (lambda (x) (* x 3))

この式を Interactions 上で評価すると、返り値が「#<procedure:5:2>」となる。これは、「関数の正体」である。

使い勝手を良くするために、次の方法で、関数の正体に名前を付けることができる。

> (define sabbai (lambda (x) (* x 3)))

ちなみに、以下の方法で、名前を付けたことが確認できる。

> sanbai

返り値が、「#<procedure:sanbai>」となるが、定義した関数の正体である。

関数を使用する

lambda 式を使用するには、コンビネーションの式を使う。以下に２通りの方法を示す。

> (sanbai 4) > ((lambda (x) (* x 3)) 4)

上記の１行目は、名前の付けられた関数を使う場合の例である。

上記の２行目は、名前の付けられていない関数を使う場合の例である。

コンビネーションの処理の内部の流れは、(1) 各部分式を評価、(2) 最左部分式の評価結果に残りの部分式の評価結果を与えて返り値を得る、である。上記１行目を評価すると、sanbai の評価値として #<procedure:sanbai> が得られ、4 の評価値として 4 が得られる。そして、4 をこの #<procedure:sanbai> に与えて返り値 12 を得ることができる。

例題１

以下の関数を定義しよう。

f(x) = 3 x + 4
g(x) = (x + 1)(x + 2)
h(x,y) = x + y

答えは以下のとおりである。

> (define f (lambda (x) (+ (* 3 x) 4))) > (define g (lambda (x) (* (+ x 1) (+ x 2)))) > (define h (lambda (x y) (+ x y)))

lambda式による順接

lambda 式の形式をよくみると、〈式1〉、〈式2〉・・・〈式n〉と、「式の並び」が定義できるようになっている。「式の並び」は、通常のプログラミングの考え方でいうところの「順接」に相当する。複数の式を持つ lambda 式の評価によって得られる返り値は、最後に評価した式〈式n〉の返り値である。

例題２

Definitions で以下を定義しよう。

(define say (lambda (x) (write "Hello ") (write x) (write "World")))

Interactions で以下を実行しよう。

> (say 'scheme)

■ 条件式

条件式は次の2つの書式がある。

(if <真偽を返す式> <真の際に評価する式> <偽の際に評価する式>) (if <真偽を返す式> <真の際に評価する式>)

ここで、２目の書式において、「真偽を返す式」が偽となった場合、評価する式が無い。したがって、返り値は不明である。しかし、処理はエラー終了とならずに進む。

if により同一の処理が可能ではあるが、Lispにおける伝統的な条件式として、cond がある。

(cond (<真偽を返す式1> <真偽を返す式1真の際に評価する式の並び1>) (<真偽を返す式2> <真偽を返す式2真の際に評価する式の並び2>) - - - (<真偽を返す式n> <真偽を返す式n真の際に評価する式の並びn>))

例題３

以下にサンプルを示す。Interactions で実行してみよう。

> (if (< 1 2) 'ok 'ng) > (if (> 1 2) 'ok 'ng) > (if (< 1 2) 'ok) > (if (> 1 2) 'ok)

■ 再帰呼び出し

ある名前で定義した関数の中で、その名前の関数を評価することを再帰呼出しという。

例題４

階乗を計算する関数 factorial を定義しよう．factorial では再帰を終了する条件は，0 の階乗を求めるときであり，その返り値は，1 である．

(define factorial (lambda (x) (if (= x 0) 1 (* x (factorial (- x 1))))))

□ 小レポート

以下の５つの関数について scheme プログラムを作成せよ。プログラムを印刷し、各行に手書きで説明を書いて、提出せよ。そして、実行の様子をスクリーンショットで画像化し、様子を手書きで説明して、提出せよ。次回 6/5 に集めます。

問１

成績を入力して、ABCラベルを出力する関数を作成しよう。もし、成績 s が 90以上ならば "A"、80以上90未満ならば "B"、70以上80未満ならば "C"、60以上70未満ならば"D"、60未満ならば"E"を返り値とせよ。ここで、if 関数を使う場合（label1 という名前を付ける)と cond 関数を使う場合 (label2 という名前を付ける) のそれぞれを作成しよう。なお、cond 関数を使う際、「#t」を条件部に置くことができる。

問２

３次方程式の解を求める関数を作成しよう。x³ - a x - b = 0 という３次方程式の解の一つは次の式で求められる。

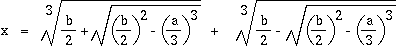
引数として、a b をとり、上記の式を計算する関数 cardano を定義せよ。

また、元の３次方程式に代入して、検算する関数 ken を定義せよ。検算では解を式に代入して計算した結果が 0 となれば ok を表示し、そうでなければ ng を表示するものとする。以下に実行例を示す。

> (cardano 25 0) 5.0+0.0i > (ken 25 0 (cardano 25 0)) ok

ちなみに、a の b 乗を計算する式は、「(expt a b)」である。

問３

ある確率を計算する関数を作成しよう。n人の人物が集まったとき、そのうち少なくとも誰か２人が同じ誕生日である確率を計算する関数 pbirthday である。この計算には、n人が全て異なる誕生日である確率を 1 から引けば良い。

たとえば、n = 3 人の場合に、3 人とも異なる誕生日であるという状況は、

365 * (365 - 1) * (365 - 2) (通り)

が存在する。全ての誕生日の状況は、365 * 365 * 365 通りであるので、3 人が全て異なる誕生日である確率は、

365 * (365 - 1) * (365 - 2) / 365 * 365 * 365

である。n人の場合の確率を一般式で表わせば次のようになる。

1 * (1 - 1/365) * (1 - 2/365) * … * (1 - (n - 1)/365)

そこで、この式に従った再帰呼び出しを利用して、全員が異なる誕生日である確率を求める関数を作成し、それを呼び出す形式で、関数 pbirthday を作成せよ。ちなみに、(pbirthday 23)は、小数に変換すると、およそ 0.507 となる（分数を小数に変換するには、exact->inexact という関数を使う「例. (exact->inexact 2/3) は 0.666...」）。意外と高い確率だ。

第7回 制御構造（5月29日）