第８回リスト（6月7日）

今日の課題

ペア
リスト

■ ペア

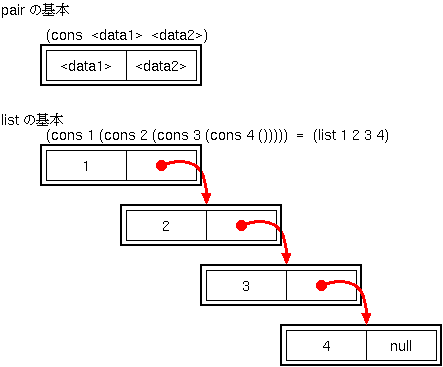
ペアとは2つのデータをまとめた構造体のことである。ドットペアと呼ばれることもある。

ペアに対する基本操作を以下にまとめる：

作成 cons: (cons 〈データ1〉〈データ2〉)
データ1の抽出 car: (car 〈ペア〉)
※ (cons 100 200)というペアのとき、返り値は 100 である。
データ2の抽出 cdr: (cdr 〈ペア〉)
※ (cons 100 200)というペアのとき、返り値は 200 である。

例題1

以下を Definitions に記述し、Run してみよう。
(define p1 (cons 100 200)) (car p1) (cdr p1)

■リスト

ペアを組み合わせて、データを並べた構造体をリストと呼ぶ。

たとえば、次のようにペアを使うと、数字のリストになる。
(define p2 (cons 1 (cons 2 (cons 3 (cons 4 ())))))

() は空を表す

このように、リストの正体は、ペアの集りであるが、分りにくい。そこで、次のように書くことができる。
(define p3 (list 1 2 3 4))

equal? を使って p2 と p3 が等しいことを確認しよう。
> (equal? p2 p3)

リストに対する基本操作を以下にまとめる：

作成 list: (list 〈データ1〉〈データ2〉 … 〈データn〉)
リストの先頭に要素を追加： (cons 〈要素〉〈リスト〉)
先頭のデータの抽出 car: (car 〈リスト〉)
※ (list 1 2 3) というリストのとき、返り値は 1 である。
2番目以降の抽出 cdr: (cdr 〈リスト〉)
※ (list 1 2 3) というリストのとき、返り値は (list 2 3) である。
　表示は (2 3) となる。
空のリストか否かの検査 null?: (null? 〈リスト〉)
※ 空のリストのとき #t （真）を返す。
リストの長さを測る関数 length: (length 〈リスト〉)
リストとリストの結合 append： (append 〈リスト1〉〈リスト2〉)
リストの持つ要素数が１つか否かの検査： (null? (cdr 〈リスト〉))

例題2

リストの個々のデータを扱う関数を作ってみよう。

数を要素とするリストを入力し、その数の総和を求める関数 list-sum
(define list-sum (lambda (lst) (if (null? lst) 0 (+ (car lst) (list-sum (cdr lst))))))
実行方法： (list-sum (list 1 2 3 4 5))
予想結果： 15

リストの個々のデータを表示する関数 list-print

(define list-print
  (lambda (lst)
    (if (not (null? lst))
        ((lambda ()                     ここの lambda は
           (write '<)                   これら write と list-print の順接を
           (write (car lst))            実行するために
           (write '>)                   使われている。
           (list-print (cdr lst)))))))  lambda の前に括弧が2つあることに注意

実行方法： (list-print (list 1 2 3 4 5))

予想結果： <1><2><3><4><5>

要素数が１個以上の数値のリストを入力として、最大値を求める関数 list-max

(define list-max
  (lambda (lst)
    (if (null? (cdr lst))           もし長さが1のリストならば、
        (car lst)                   リストの先頭の数値が最大値である。
        ((lambda (m n)              そうでなければ、2つの数値 m と n について
           (if (> m n) m n))        大きい数値を返す関数に、
         (car lst)                  リストの先頭の数値と
         (list-max (cdr lst))))))   リストの2番目以降の最大値を比較してもらう。

実行方法： (list-max (list 1 2 4 5 3))

予想結果： 5

上記の list-max の意味がわからない人は以下の定義をまず考えてみよう。
(define greater (lambda (m n) (if (> m n) m n))) (define list-max (lambda (lst) (if (null? (cdr lst)) (car lst) (greater (car lst) (list-max (cdr lst))))))

以下の定義でも動作する。

ところで、関数型言語ならば、引数が同じ関数呼出しは同じ答えが得られるはずだから、無駄な計算は発生しない？ ⇒ ダウト。その保証はない！悩んでください。
(define list-max (lambda (lst) (if (null? (cdr lst)) (car lst) (if (> (car lst) (list-max (cdr lst))) (car lst) (list-max (cdr lst))))))

上記の例は、リストから値を抽出する関数であった。次にリストを返す関数を作ってみよう。

例題3

append 関数は、drscheme に組み込み関数として既に用意されている。ここでは練習のために、自分で cons を用いて定義しよう。自分で作った append 関数を my-append とする。
(define my-append (lambda (lst1 lst2) (if (null? lst1) lst2 (cons (car lst1) (my-append (cdr lst1) lst2)))))
実行方法： (my-append (list 1 2 3) (list 4 5 6))
予想結果： (1 2 3 4 5 6)
実行方法： (my-append (cons 1 (cons 2 ())) (cons 3 (cons 4 ())))
予想結果： (1 2 3 4)
数値のリストを入力して、各値が 2 倍となった新しいリストを帰す関数 list-double を定義しよう．
(define list-double (lambda (lst) (if (null? lst) () ← 空を表す。(list) と同じ。 (cons (* 2 (car lst)) (list-double (cdr lst))))))
実行方法： (list-double (list 1 2 3 4 5))
予想結果： (2 4 6 8 10)
入力される数値のリストから次のリストを作る関数 add-next を定義しよう：
新しく作られるリストの各数値は、入力のリストの要素において隣り合う2つの数値の和とする。たとえば，(1 1) を入力すると (2) を返し、(1 2 1) を入力すると (3 3)を返す。
ただし、入力のリストの要素数が2未満のときは空のリストを返すこととする。
(define add-next (lambda (lst) (if (< (length lst) 2) (list ) (cons (+ (car lst) (car (cdr lst))) (add-next (cdr lst))))))
実行方法： (add-next (list 1 2 1))
予想結果： (3 3)

■ 練習問題

練習1：ドリル

リスト操作と再帰呼出しに慣れるために、以下の関数を作ってみよう。できるところからやってみよう。

easy level

問１：(sum 〈数値のリスト〉)：数値のリストを入力し、その中の数値の合計を返す。
問２：(size 〈リスト〉)：リストの要素数を返す。
問３：(average 〈数値のリスト〉)：数値のリストを入力し、平均値を返す。
問４：(even 〈数値のリスト〉）：数値のリストを入力し、その中の偶数値だけのリストを作って返す。（ヒント：数値が偶数であることを判定する関数 even? は既に存在する。例、(even? 4) ⇒ #t）

enjoy level

問５：(skip 〈リスト〉) ：リストを入力し、奇数番目の要素をリストに入れて返す。例：(skip (list 'a 'b 'c)) ⇒ (list 'a 'c)、(skip (list 'a 'b 'c 'd)) ⇒ (list 'a 'c)
問６：(my-reverse 〈リスト〉)：リストの要素の順序を逆順にしたものを返す。例：(my-reverse (list 1 2 3)) ⇒ (list 3 2 1)
問７：(draw-four 〈数値のリスト〉)：数値のリストを入力し、4 が最も連続する部分を抽出し、その合計値を返す。例：(draw-four (list 1 2 3 4 4 2 3)) ⇒ 8、(draw-four (list 1 2)) ⇒ 0、(draw-four (list 1 4 4 3 4 4 4 2)) ⇒ 12、(draw-four (list 1 4 4 3 4 4 4)) ⇒ 12

ヒント：1 つの問につき、関数を 2 つ作ると簡単。

練習2：A4用紙のサイズ

よく使うプリンタの用紙は、A4サイズである（210mm x 297mm）。この用紙は、長辺を半分に折るとA5サイズの用紙になる（小数点の切り捨てはtruncate関数を使用）。A0サイズは、841mm x 1189mm という大きさである。では、nを変数として Anサイズの2辺の長さをペアの値で返す関数 (paper-a-size n) を定義せよ。

ヒント：ペアのデータ1を短辺、データ2を長辺とすることにする。

ヒント：ペアのデータを入力として、長辺を折り曲げて新しい短辺とし、短辺を新しい長辺としてペアの値を返す関数を作ってみる。

練習3：パスカルの三角形 (normal)

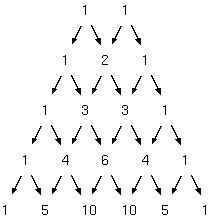
問題を説明する前に、次の式を見てみよう。

(a+b)¹ = a + b

(a+b)² = a² + 2ab + b²

(a+b)³ = a³ + 3a²b + 3ab² + b³

(a+b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a+b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

右辺の係数に注目すると、次の図のような関係が見えてくる。この図をパスカルの三角形という。

(a+b)の羃乗の数ごとに、係数をリストで表すと、次のようになる。

(a+b)¹のとき (list 1 1)

(a+b)²のとき (list 1 2 1)

(a+b)³のとき (list 1 3 3 1)

(a+b)⁴のとき (list 1 4 6 4 1)

(a+b)ⁿのときの係数のリストを返す関数 list-pascal(n) を定義せよ。

ヒント：list-pascal では、n = 1 のとき、「(list 1 1)を返すこと」として、そのほかのとき、「n - 1 の list-pascal の返り値について add-next を計算した結果の前後に 1 を付けたもの」とするとよい。つまり，n=3 の (1 3 3 1) を求める計算では、n=2 の list-pascal の返り値である (1 2 1) から、add-next を用いて (3 3) を求めて、前後に (1) を append すると実現できる。

できた人は、append を使わずに、cons を使って関数 list-pascal を定義しよう。

（注意：add-next の使用は各自の自由である。）

第８回 リスト（6月7日）