第８回 リスト（6月8日）

今日の課題

• ペア（コンス）
• リスト

■ ペア（コンス）

2つのデータをまとめたもの．通常は後述するリストを使用することが好まれる．

コンスに対する基本操作を以下にまとめる：

• 作成 cons: (cons 〈データ1〉 〈データ2〉)
• データ1の抽出 car: (car x) ※ 変数xに(cons 100 200)がバインドされているとき，(car x)の返り値は 100 である．
• データ2の抽出 cdr: (cdr x) ※ 変数xに(cons 100 200)がバインドされているとき，(car x)の返り値は 200 である．

例題1

以下を Definitions に記述し，Run してみよう．

(define p1 (cons 100 200)) (car p1) (cdr p1)

■リスト

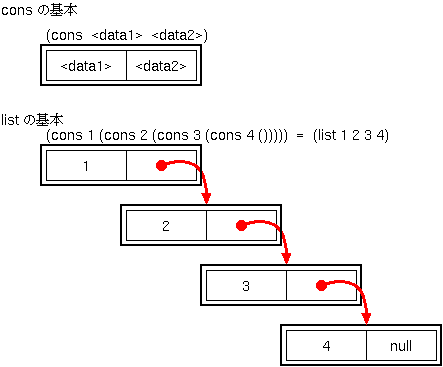
コンスを組み合わせて，データを並べたものがリストである．

リストに対する基本操作を以下にまとめる：

• 作成 list: (list 〈データ1〉 〈データ2〉 … 〈データn〉)
• リストの先頭に要素を追加： (cons elem lst)
• 先頭のデータの抽出 car: (car lst) ※ 変数 lst に (list 1 2 3) がバインドされているとき，返り値は 1 である．
• 2番目以降の抽出 cdr: (cdr lst) ※ 変数 lst に (list 1 2 3) がバインドされているとき，返り値は (list 2 3) である（表示は (2 3) となる）．
• 空のリストか否かの検査 null?: (null? lst) ※ 変数 lst がデータを持たないとき #t （真）を返す（要素が1つのリストに cdr をすると返り値は null））．
• リストの長さを測る関数 length: (length lst)
• リストとリストの結合 append： (append lst1 lst2)

例題2

リストの個々のデータを扱う関数を作ってみよう．

1. 数を要素とするリストを入力し，その数の総和を求める関数 sum-list

   実行方法： (sum-list (list 1 2 3 4 5))

   (define sum-list (lambda (lst) (if (null? lst) 0 (+ (car lst) (sum-list (cdr lst))))))

2. リストの個々のデータを表示する関数 print-list

   実行方法： (print-list (list 1 2 3 4 5))

   (define print-list (lambda (lst) (if (not (null? lst)) ((lambda () ここの lambda は (write '<) これら write と print-list の順接を (write (car lst)) 実行するために (write '>) 使われている． (print-list (cdr lst))))))) lambda の前に括弧が2つあることに注意

3. 数を要素とするリストを入力し，最大値を求める関数 max-list

   実行方法： (max-list (list 1 2 4 5 3))

   (define max-list (lambda (lst) (if (= 1 (length lst)) もし長さが1のリストならば， (car lst) リストの先頭の数値が最大値 ((lambda (m n) そうでなければ，2つの数値 m と n について (if (> m n) m n)) 大きい数値を返す関数に， (car lst) リストの先頭の数値と (max-list (cdr lst)))))) リストの2番目以降の最大値を比較してもらう．

   上記の max-list の意味がわからない人は以下の定義をまず考えてみよう．

   (define max-list01 (lambda (m n) (if (> m n) m n))) (define max-list (lambda (lst) (if (= 1 (length lst)) (car lst) (max-list01 (car lst) (max-list (cdr lst))))))

   以下の定義でも動作するが，無駄が多い？ 関数型言語ならば，引数が同じ関数呼出しは同じ答えが得られるはずであり，無駄な計算はないので，無駄にはならない？

   (define max-list (lambda (lst) (if (= 1 (length lst)) (car lst) (if (> (car lst) (max-list (cdr lst))) (car lst) (max-list (cdr lst))))))

上記の例は，リストから値を抽出する関数であった．次にリストを加工してみよう．

例題3

1. append 関数を cons を用いて定義しよう．自分で作った append 関数を my-append とする．

   実行方法： (my-append (list 1 2 3) (list 4 5 6))

   (define my-append (lambda (lst1 lst2) (if (null? lst1) lst2 (cons (car lst1) (my-append (cdr lst1) lst2)))))

2. リスト内の各数値を 2 倍にする関数 double を定義しよう．

   実行方法： (double (list 1 2 3 4 5))

   (define double (lambda (lst) (if (null? lst) (list ) (cons (* 2 (car lst)) (double (cdr lst))))))

3. 数を格納したリストから次のようなリストを作る関数 add-next を定義しよう：新しいリストは，入力のリストの隣り合う2つの数値の和とする．たとえば，(1 1) を入力すると (2) を返し，(1 2 1) を入力すると (3 3)を返す．また，入力のリストは要素数が2未満のときは空のリストとする．

   実行方法： (add-next (list 1 2 1))

   (define add-next (lambda (lst) (if (< (length lst) 2) (list ) (cons (+ (car lst) (car (cdr lst))) (add-next (cdr lst))))))

■ 練習問題

練習1：A4用紙のサイズ

よく使うプリンタの用紙は，A4サイズである（210mm x 297mm）．この用 紙は，長辺を半分に折るとA5サイズの用紙になる（小数点は切り捨て． truncate関数）．A0サイズは，841mm x 1189mm という大きさである．では， nを変数として Anサイズの2辺の長さをペアの値で返す関数 (paper-a-size n) を定義せよ．

ヒント：ペアのデータ1を短辺，データ2を長辺とすることにする．

ヒント：ペアのデータを入力として，長辺を折り曲げて新しい短辺とし，短辺を新しい長辺としてペアの値を返す関数を作ってみる．

練習2：パスカルの三角形

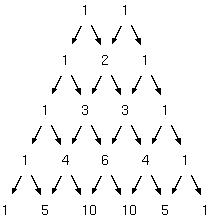
問題を説明する前に，次の式を見てみよう．

(a+b)¹ = a + b

(a+b)² = a² + 2ab + b²

(a+b)³ = a³ + 3a²b + 3ab² + b³

(a+b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a+b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

:

右辺の係数に注目すると，次の図のような関係が見えてくる．この図をパスカルの三角形という．

(a+b)の羃乗の数ごとに，係数をリストで表すと，次のようになる．

(a+b)¹のとき (list 1 1)

(a+b)²のとき (list 1 2 1)

(a+b)³のとき (list 1 3 3 1)

(a+b)⁴のとき (list 1 4 6 4 1)

(a+b)ⁿのときの係数のリストを返す関数 pascal-list を定義せよ．

ヒント：pascal-list では，n = 1 のとき，「(list 1 1)を返すこと」として，そのほかのとき，「先頭が 1 であり，そして，残りが n - 1 の pascal-list の返り値について add-next のような計算をしたもの」とするとよい．つまり，(1 3 3 1)を求める計算では，(1 2 1)から(3 3)を求めて，前後に (1) を append すると実現できる．

できた人は，append を使わずに，cons を使って関数 pascal-list を定義しよう．