


�$B Speaker Classification Problem
�$B>e$X�(B: Estimation of optimal state
�$BLa$k�(B: Viterbi algorithm
To estimate the optimal state sequence, we propose the new algorithm called the forward
algorithm.
This algorithm summarizes the likelihood for all
states. The optimal state sequence is then chosen as the
maximum likelihood state at each time (frame).
This forward algorithm is described as follows.
- For all
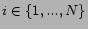 , let
, let
- Along the time axis
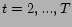 , for all
, for all
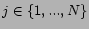 , let
, let
- The likelihood
for all possible state transition sequences and the optimal state at time
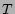 are given as follows.
are given as follows.
Jin'ichi Murakami
�$BJ?@.�(B13�$BG/�(B1�$B7n�(B19�$BF|�(B