従来手法との比較

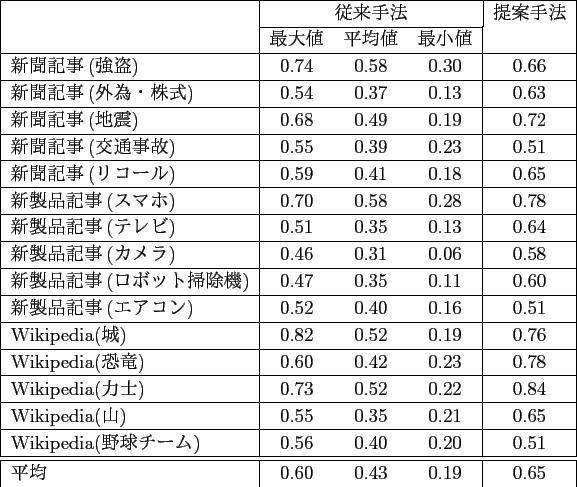15種類の複数文書を用いた実験では，提案手法の評価結果の平均が0.65と従来手法の最大値，平均値を上回る結果となった． また，有意水準を0.05として対応のある両側$t$検定を行った結果，従来手法と提案手法の評価結果の間に有意差があるという結果が得られた． 提案手法では表の埋まり具合と情報の密集度のバランスを最適にすることで，表の整理により適したクラスタ数(表の列数)の推定を行うことができ，この結果，表の精度を向上させることができたと思われる．

実際に，従来手法と提案手法でそれぞれ推定されたクラスタ数(表の列数)と，正解の表の列数を比較した結果，表5.1のようになった． また，従来手法と提案手法でそれぞれ推定されたクラスタ数(表の列数)と，正解の表の列数の差の絶対値を比較した結果は，表5.2のようになった． 結果から，従来手法では,正解の表の列数との差が平均で6.7あったが，提案手法ではこの差が3.8に縮まった． よって，従来手法において，$X$-means法により推定されたクラスタ数(表の列数)が小さい傾向にあった問題は提案手法では改善され， より正解の表の列数に近づいたことが分かった．

また，今回，表の精度を表の各列の$F値$の平均として求めたが，このときの各列の適合率の平均と再現率の平均を求めたところ， 表5.3のような結果が得られた．表5.3より，従来手法の平均値での結果では，再現率が平均で0.79であるのに対し，適合率が平均で0.39と低い． これは，従来手法で得られる表の列の特徴が，情報の取りこぼしが少ない一方で関連しない情報を含みやすいことを示している． 一方で，提案手法では，再現率が平均で0.68であるのに対し，適合率が平均で0.75であり，二つの指標の隔たりが小さいため， バランスの良い表が得られていることが分かる．

表: 生成された表の列数

表: 最適な表の列数との差

表: 表の再現率(平均)と適合率(平均)