従来手法の問題点

情報を表に整理する場合，表2.2の列1のように情報が1列にまとまりすぎたり，表2.3の列2，列3のように情報が細かく分類されすぎることのない，表2.4のようなバランスの良い表が望ましいと考えられる．一方で，従来手法では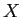

-means法によって推定されたクラスタ数(表の列数)が最適なクラスタ数に比べに小さい傾向にあった．この結果，表2.2の列1でメモリーの情報とストレージの情報が混在しているような，情報が1つの列にまとまりすぎた表が得られることが多く，このことが表の精度が低い原因であった．

表の精度を向上させるためには，表2.2や表2.3のいずれにも偏ることなく，これらのバランスを最適にするような結果が得られるようにクラスタ数(列数)を推定する必要がある．

表: 情報が1列にまとまりすぎた例

列1

列2

メモリーは4GB

内蔵ストレージは64GB

発売日は10月上旬

メモリーが3GB

ストレージが32GB

発売日は9月

メモリーが3GB

内蔵ストレージが32GB

発売日は1月

メモリーが3GB

内蔵ストレージが32GB

8月より発売