


Next: seq2seq
Up: ニューラルネットワーク
Previous: RNN
目次
RNNの過去の出力は時刻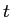 が進んでいく(ニューラルネットの層が深くなる)と,古い過去の出力が
反映されなくなる.長期にわたり過去の出力を保持するための方法の1つがLSTMである.
図2.2にLSTMの内部構造を示す.
中央にメモリセル(図中記号a)がある.メモリセルは状態
が進んでいく(ニューラルネットの層が深くなる)と,古い過去の出力が
反映されなくなる.長期にわたり過去の出力を保持するための方法の1つがLSTMである.
図2.2にLSTMの内部構造を示す.
中央にメモリセル(図中記号a)がある.メモリセルは状態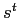 を保持し,1時刻を隔てて
メモリセル自身に
を保持し,1時刻を隔てて
メモリセル自身に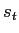 (帰還時は
(帰還時は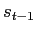 )を帰還させる.
周囲に5つのユニット(図中記号b〜f)と3つのゲート(入力ゲート,忘却ゲート,出力ゲート)がある.
ユニットc,d,fは,
)を帰還させる.
周囲に5つのユニット(図中記号b〜f)と3つのゲート(入力ゲート,忘却ゲート,出力ゲート)がある.
ユニットc,d,fは,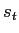 ,
,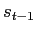 にパラメータ(重み)を掛け,
外部からの入力
にパラメータ(重み)を掛け,
外部からの入力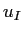 ,
,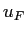 ,
,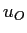 と足しあわせ,活性化関数(ロジスティックシグモイド関数)
と足しあわせ,活性化関数(ロジスティックシグモイド関数)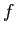 を適用したものを
各ゲートに出力する.
ユニットbは前の層からの入力
を適用したものを
各ゲートに出力する.
ユニットbは前の層からの入力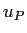 を受けとり,活性化関数
を受けとり,活性化関数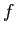 を適用する.
入力
を適用する.
入力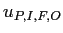 は以下の式で表される.
は以下の式で表される.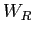 は帰還値の重みである.
は帰還値の重みである.
ゲートはそれぞれゲート値を持つ.ゲート値は活性化関数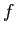 により値域を[0,1]に制約され,
この値が1の時にデータが伝達される.
各ゲートの出力値は以下の式で表される.
により値域を[0,1]に制約され,
この値が1の時にデータが伝達される.
各ゲートの出力値は以下の式で表される.
ユニットeはメモリセルの出力に活性化関数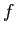 を適用する.
状態
を適用する.
状態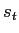 と出力
と出力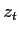 は以下のように表される[3].
は以下のように表される[3].
2018-02-28